Предмет: Математика,
автор: baljanjeksenbai1
5.72. Разложите многочлен на множители:
1) х³+у³;
4) m³+n³;
7) a³+8;
2) х³-у³;
5) р³+q³;
8) а³-8;
3) m³-n³;
6) р³-q³;
9) m³+27;
10) n³-27;
11) 1-x³;
12) 1+у³.
Приложения:

Ответы
Автор ответа:
13
Пошаговое объяснение:
Для разложения на множители воспользуемся формулами
Автор ответа:
4
Ответ: на фото.
Задания сделаны по формуле суммы и разности кубов двух выражений.
Приложения:
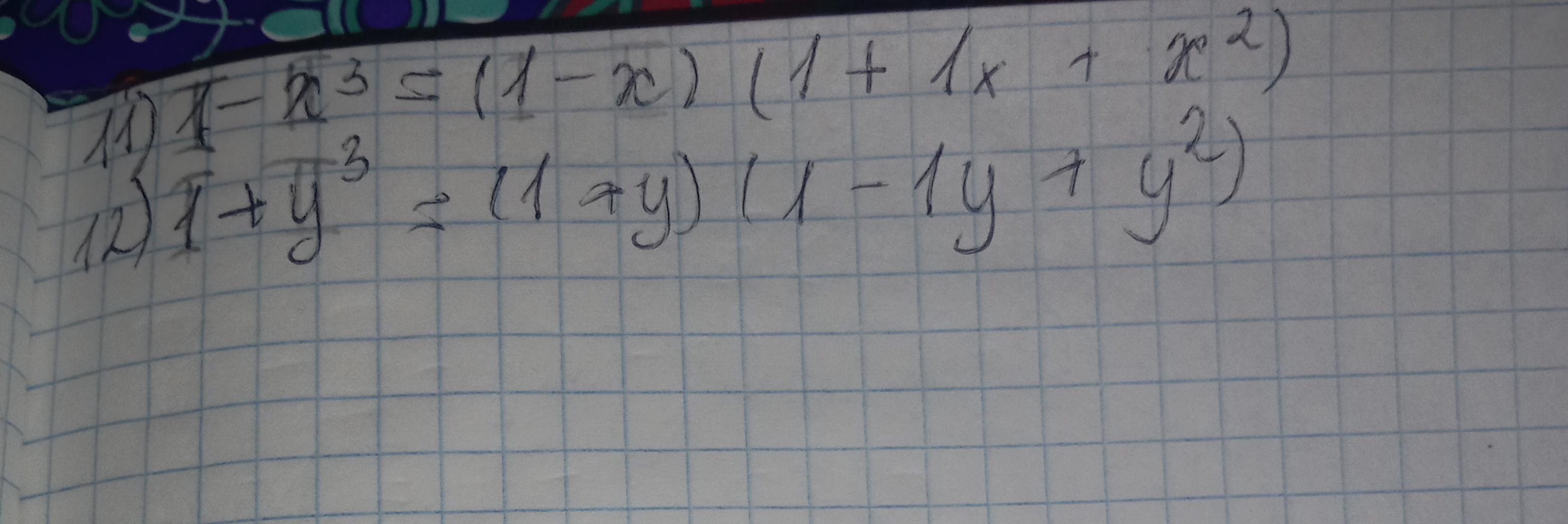

Похожие вопросы
Предмет: Математика,
автор: wowinc
Предмет: Математика,
автор: smonarh
Предмет: Русский язык,
автор: clevtzovalyuda12
Предмет: Математика,
автор: levyska2005p3ixbi
Предмет: Математика,
автор: тимыч7