Question

Пожалуйста помогите, даю много баллов!!! СРОЧНО НУЖНО РЕШЕНИЕ, ЧТОБЫ ПОНЯТНО!!!!!!

Answer 1

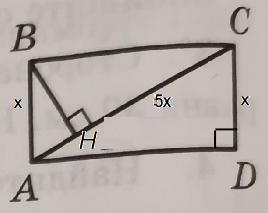
На рисунке  ABCD – прямоугольник, ВН перпендикулярен АС, сторона АВ в 5 раз меньше диагонали. Найдите ВН, если AD=12

Ответ: 2,4 (ед. длины)

Объяснение:

Примем AB=х.Так как АВСD –прямоугольник, СD=AB. По т.Пифагора АC²=AD²+CD^2⇒

25х²=144+х²

24х²=144

х²=6

АВ=х=√6

АС=5√6

ВН - высота треугольника АВС. Высота прямоугольного треугольника, проведенная к гипотенузе,  делит его на два подобных друг другу и исходному.

    Задачу можно решить через подобие ∆ АВС и ∆ АВН, но можно из площади ∆ АВС.

Ѕ(АВС)=АВ•ВС•1/2=ВН•АС•1/2, откуда ВН=2Ѕ(АВС):АС

ВН=12•√6:5√6=2,4 (ед. длины)