Предмет: Алгебра,
автор: nurikkk
Помогите. Интегралы, даю 40 баллов
Приложения:



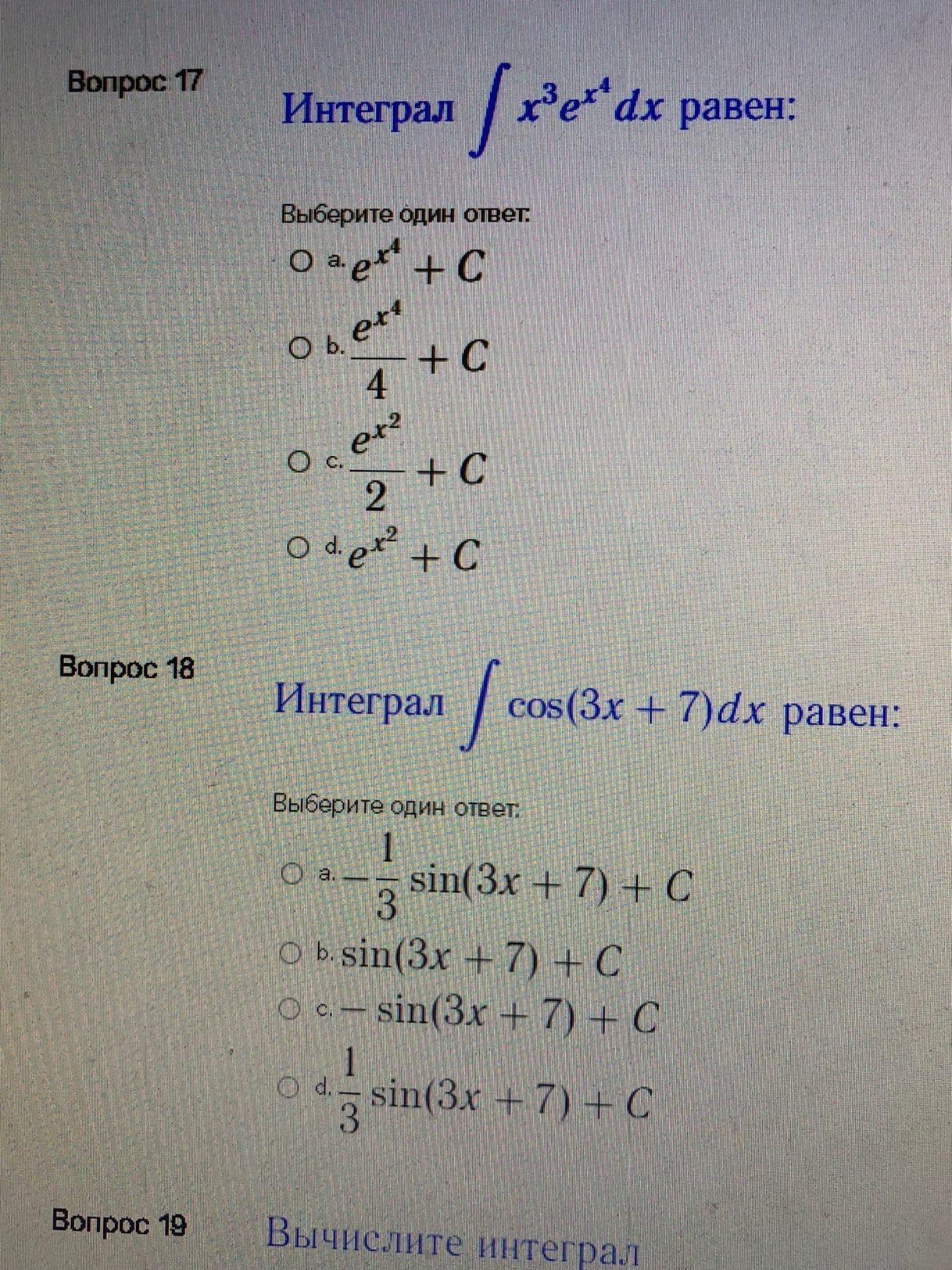
Ответы
Автор ответа:
1
9.
Ответ: 3
10.
Ответ: 3
19.
Ответ: d
20.
Ответ: d
15.
Ответ: d
16.
Ответ: а
17.
Ответ: b
18.
Ответ: d
Похожие вопросы
Предмет: Алгебра,
автор: 11194
Предмет: Математика,
автор: ванёк20005
Предмет: Математика,
автор: ladi02
Предмет: Литература,
автор: drlol1