Предмет: Геометрия,
автор: borzova16
При каких значениях угла треугольника квадрат стороны, лежащей против этого угла: а) меньше суммы квадратов двух других сторон;
б) равен сумме квадратов двух других сторон;
в) больше суммы квадратов двух других сторон?
Ответы
Автор ответа:
6
Ответ:
а) 0° < ∠BAC < 90°
б) ∠BAC = 90°
в) 90° < ∠BAC < 180°
Объяснение:
По теореме косинусов:
а) Если угол 0° < ∠BAC < 90°, то от выражению мы отнимаем
так как косинус больше нуля.
б) при
, то есть при
.
в) Если угол 90° < ∠BAC < 180°, то к выражению мы прибавляем
так как косинус меньше нуля.
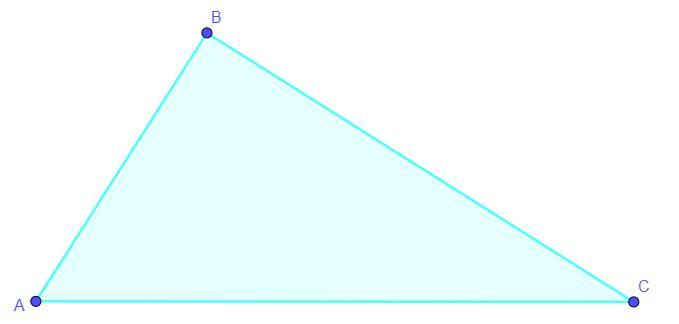
Приложения:
Похожие вопросы
Предмет: География,
автор: CHIAURELY
Предмет: Алгебра,
автор: remizovrodion1
Предмет: Русский язык,
автор: Ulka556
Предмет: Математика,
автор: аселешка
Предмет: Математика,
автор: kisks27