Предмет: Математика,
автор: aaa03
Составить дифференциал второго порядка функции.
Приложения:
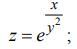
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Физика,
автор: fiti01
Предмет: Математика,
автор: LizaLebedevaAngel
Предмет: Русский язык,
автор: msmaks12
Предмет: Геометрия,
автор: xxx1111000
Предмет: Биология,
автор: Анастасия0708