Предмет: Математика,
автор: shevtsovajul8
Помогите пожалуйста.
Найти решение задачи Коши.
Приложения:
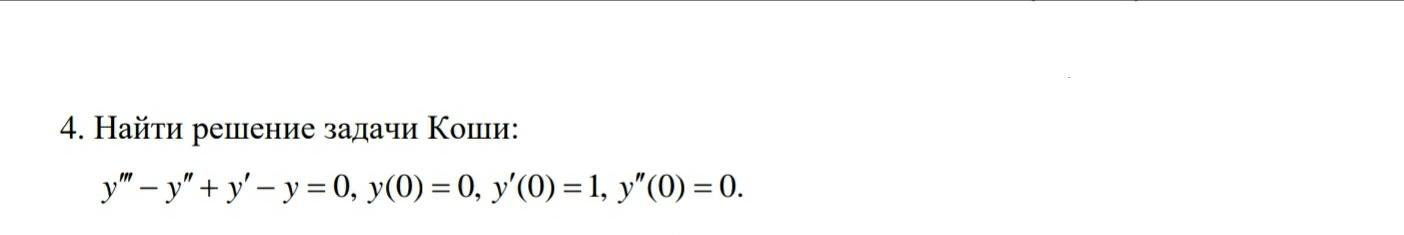
Ответы
Автор ответа:
2
Ответ:
общее решение
система:
частное решение
shevtsovajul8:
Спасибо большое))
Похожие вопросы
Предмет: Математика,
автор: Deva12
Предмет: Українська мова,
автор: konfetkaua1
Предмет: Физика,
автор: nina19983
Предмет: Математика,
автор: KatyaRomanovna
Предмет: Биология,
автор: окоеоер