Question

Знайдітб об'єм правильної трикутної піраміди бічне ребро якої дорівнює 7см. а сторона основи 2√3​

Answer 1

Ответ:

3√15 см³.

Объяснение:

Объем пирамиды определяется по формуле:

$V=\dfrac{1}{3} \cdot S\cdot H$

где S- площадь основания,  H - высота пирамиды.

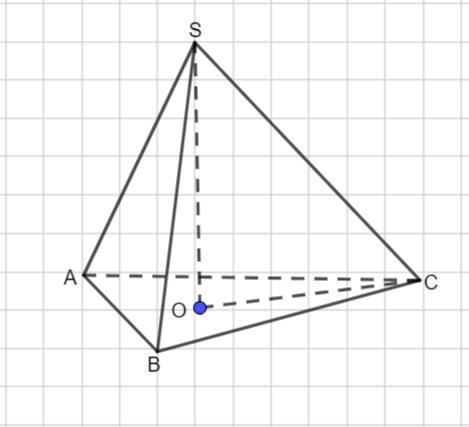
Так как пирамида правильная, то в основании треугольник АВС - правильный, площадь которого можно найти по формуле:

$S=\dfrac{a^{2} \sqrt{3} }{4} ,$

где а -сторона треугольника.

$a=2\sqrt{3}; \\\\S= \dfrac{(2\sqrt{3})^{2} \cdot\sqrt{3} }{4} =\dfrac{4\cdot3\cdot \sqrt{3} }{4} =3\sqrt{3}$

Тогда площадь основания равна 3√3 см².

SO- высота пирамиды. Рассмотрим треугольник SOC - прямоугольный.

$OC=R =\dfrac{a}{\sqrt{3} } ;\\OC=\dfrac{2\sqrt{3} }{\sqrt{3} } =2.$

По теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

$SC^{2} =SO^{2} +OC^{2} ;\\SO^{2} =SC^{2} -OC^{2};\\SO= \sqrt{SC^{2} -OC^{2}} ;\\SO= \sqrt{7^{2} -2^{2} } =\sqrt{49-4} =\sqrt{45} =\sqrt{9\cdot5} =3\sqrt{5}$.

Тогда найдем объем пирамиды.

$V=\dfrac{1}{3} \cdot 3\sqrt{3} \cdot3\sqrt{5} =3\sqrt{15}$

Объем пирамиды равен 3√15 см³