Предмет: Алгебра,
автор: dimoncoolgamer
Упростите выражения, срочно
(Пишите где какой номер выражения)
Приложения:
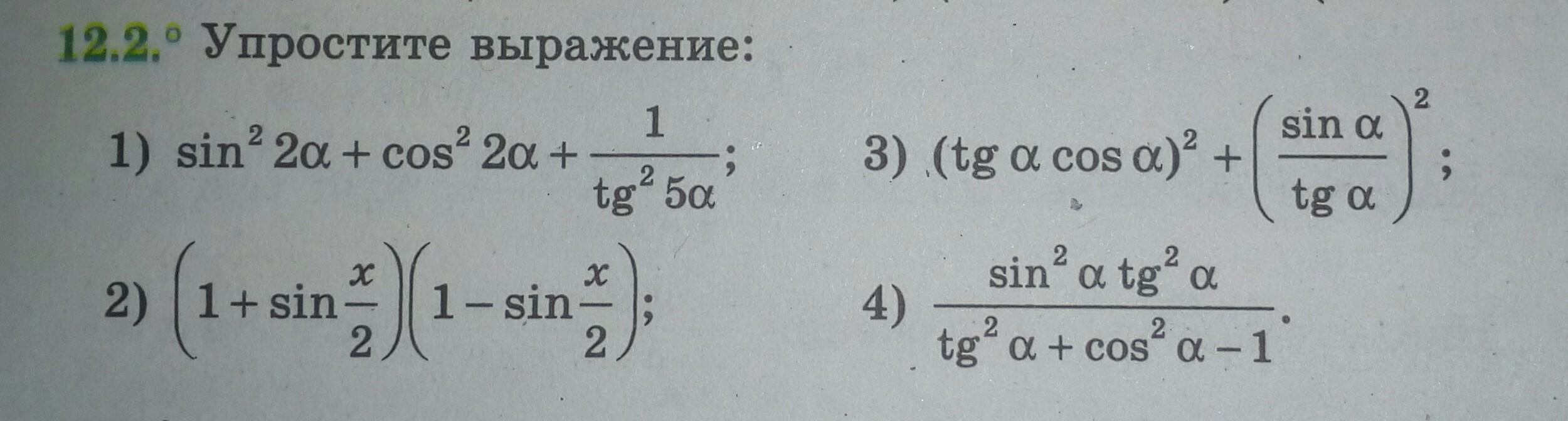
Ответы
Автор ответа:
1
Ответ:
12.2
1.
2.
3.
4.
4.
Похожие вопросы
Предмет: Литература,
автор: reginysha
Предмет: Физика,
автор: nyurgunkhalyev
Предмет: Биология,
автор: Vera543
Предмет: Алгебра,
автор: Сан81