Предмет: Математика,
автор: VladSM21
тригонометричні нерівноті!
алгебра 10 клас срочно!
Приложения:

Ответы
Автор ответа:
3
Ответ:
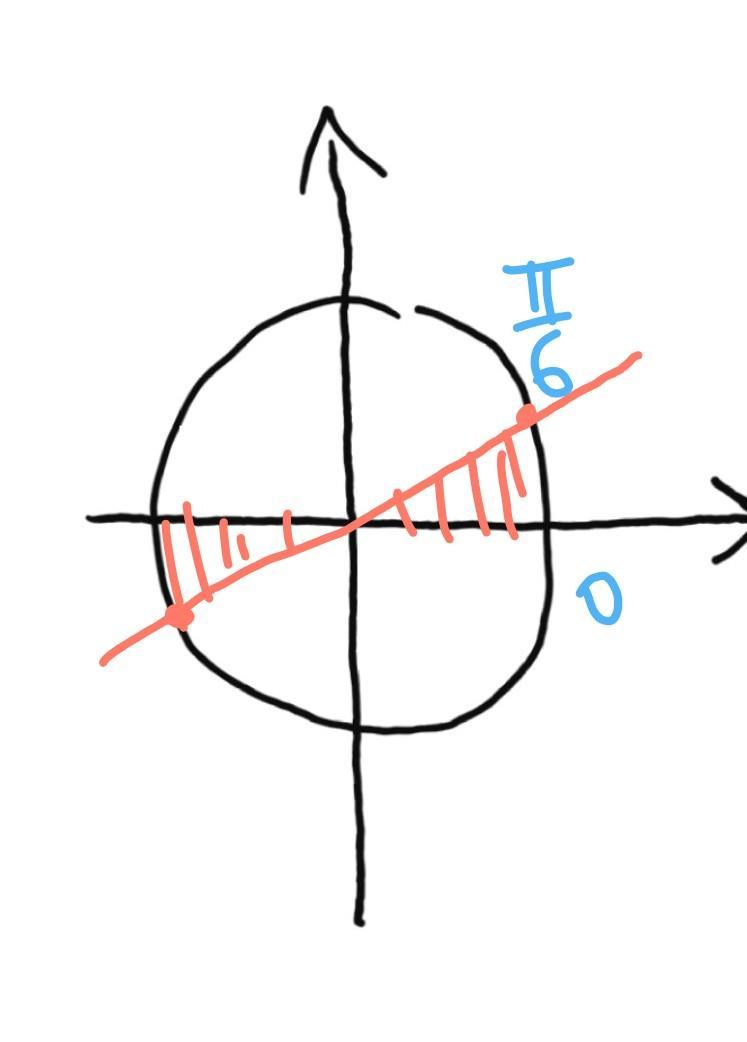
1.
рисунок1
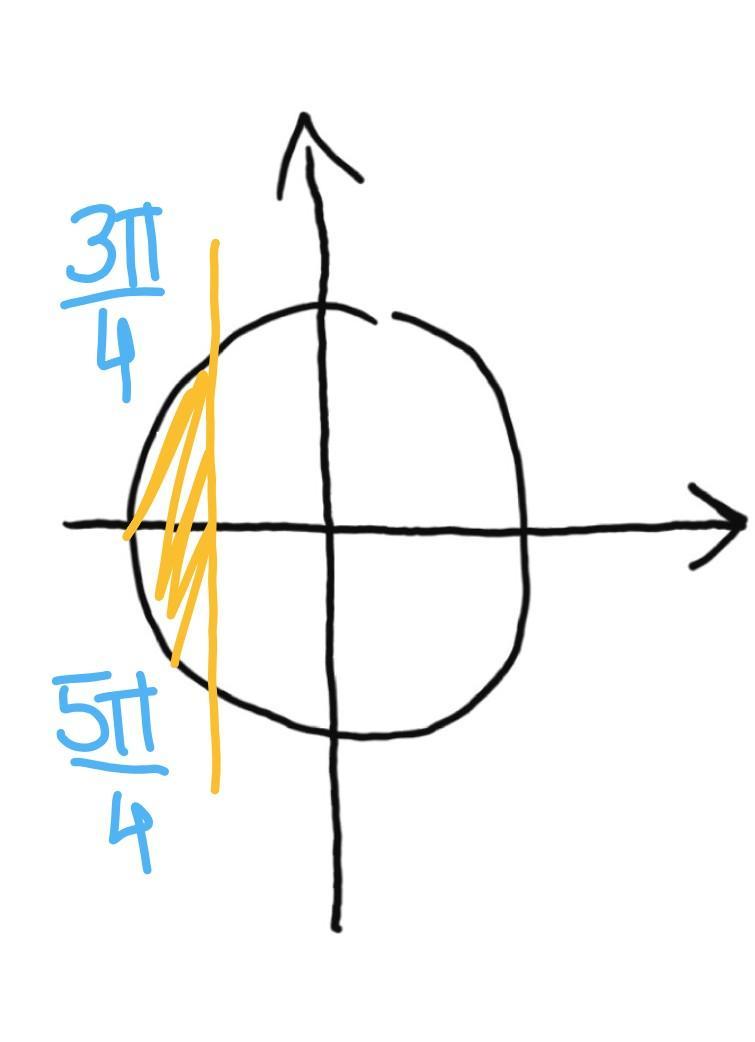
2.
рисунок2
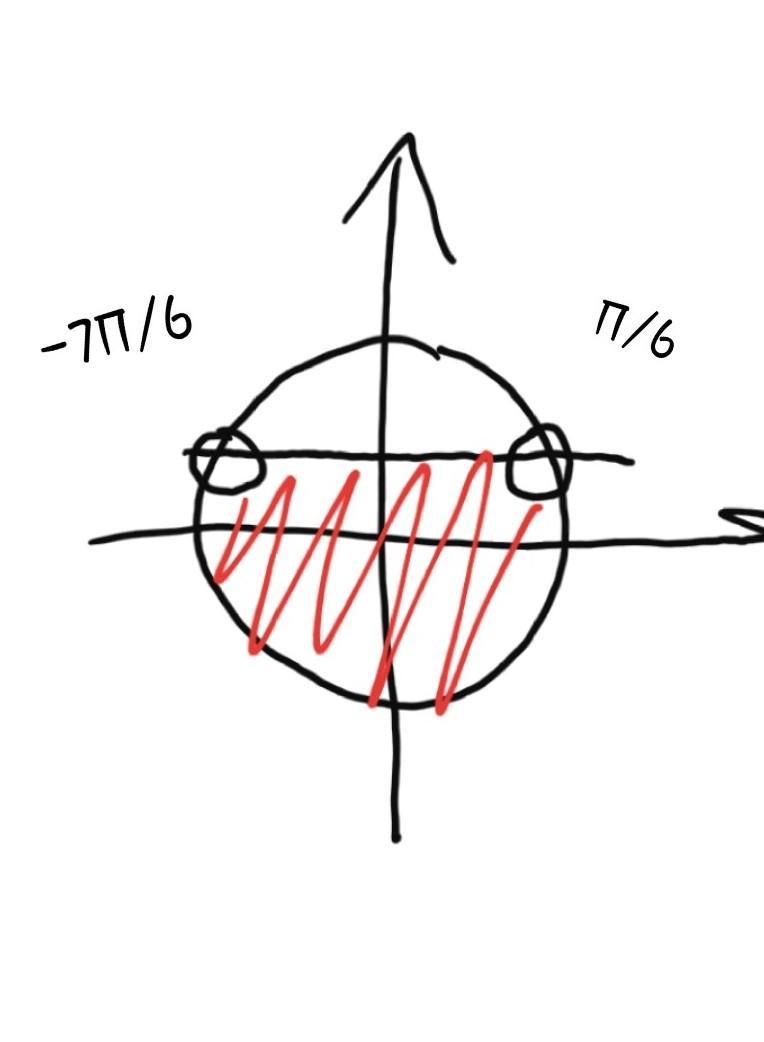
3.
рисунок 3
n принадлежит Z.
Приложения:
aulymkuanbaj:
Miroslava227 помагите пожалуйста с русским языком в профиле
Похожие вопросы
Предмет: Математика,
автор: wictor201019722010
Предмет: Русский язык,
автор: REDFREEDOM
Предмет: Математика,
автор: dilso
Предмет: Литература,
автор: Kirillleo2002
Предмет: Химия,
автор: Sjsjssj