Предмет: Алгебра,
автор: alenmilovich
помогите решить
sin(P-2x) =cos^2x [-P/2;3P/2)]
Ответы
Автор ответа:
1
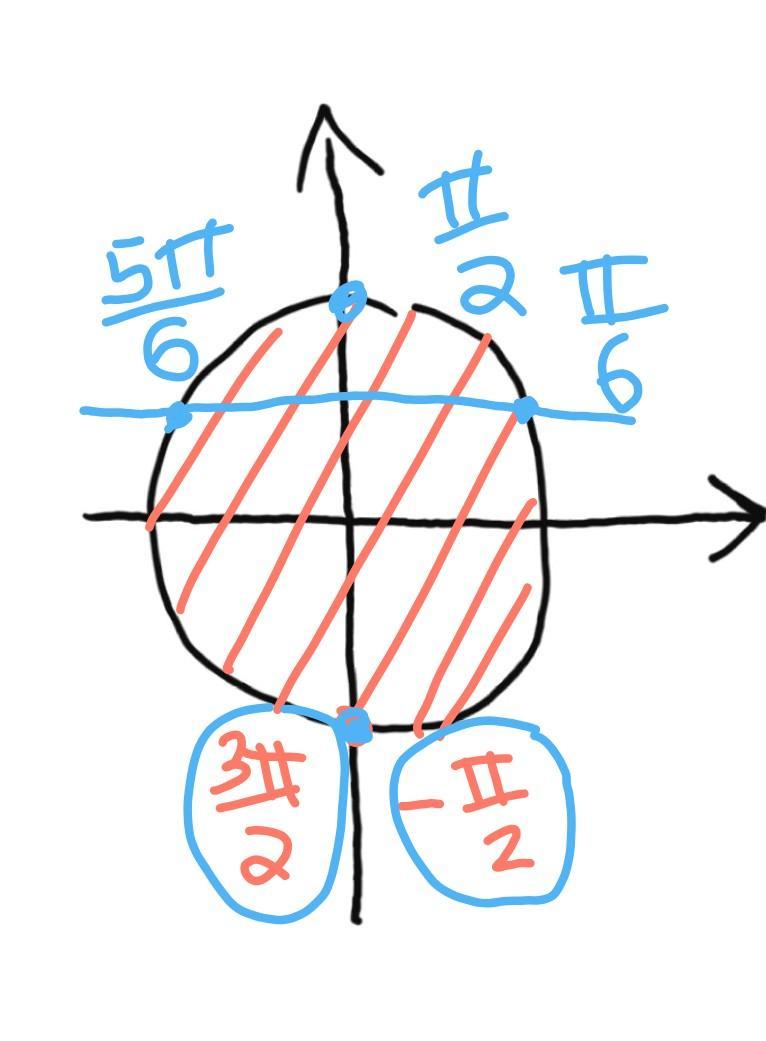
Ответ:
n принадлежит Z.
Ответ:
Приложения:
alenmilovich:
ого‚ спасибо‚ буду разбираться
Похожие вопросы
Предмет: Литература,
автор: олег20015
Предмет: Математика,
автор: ErikGag
Предмет: Биология,
автор: tdolgova
Предмет: История,
автор: Vglynin2208