Предмет: Алгебра,
автор: kolosokelizaveta
60 баллов!!!!!!Ребята,помогите пожалуйста.очень срочно нужно.кому не сложно.могу добавить ещё 40 баллов с помощью загадки за правильный ответ..позязя
Приложения:
kolosokelizaveta:
Я добавлю вопрос на 40 б,там будет загадка.Помогитеее
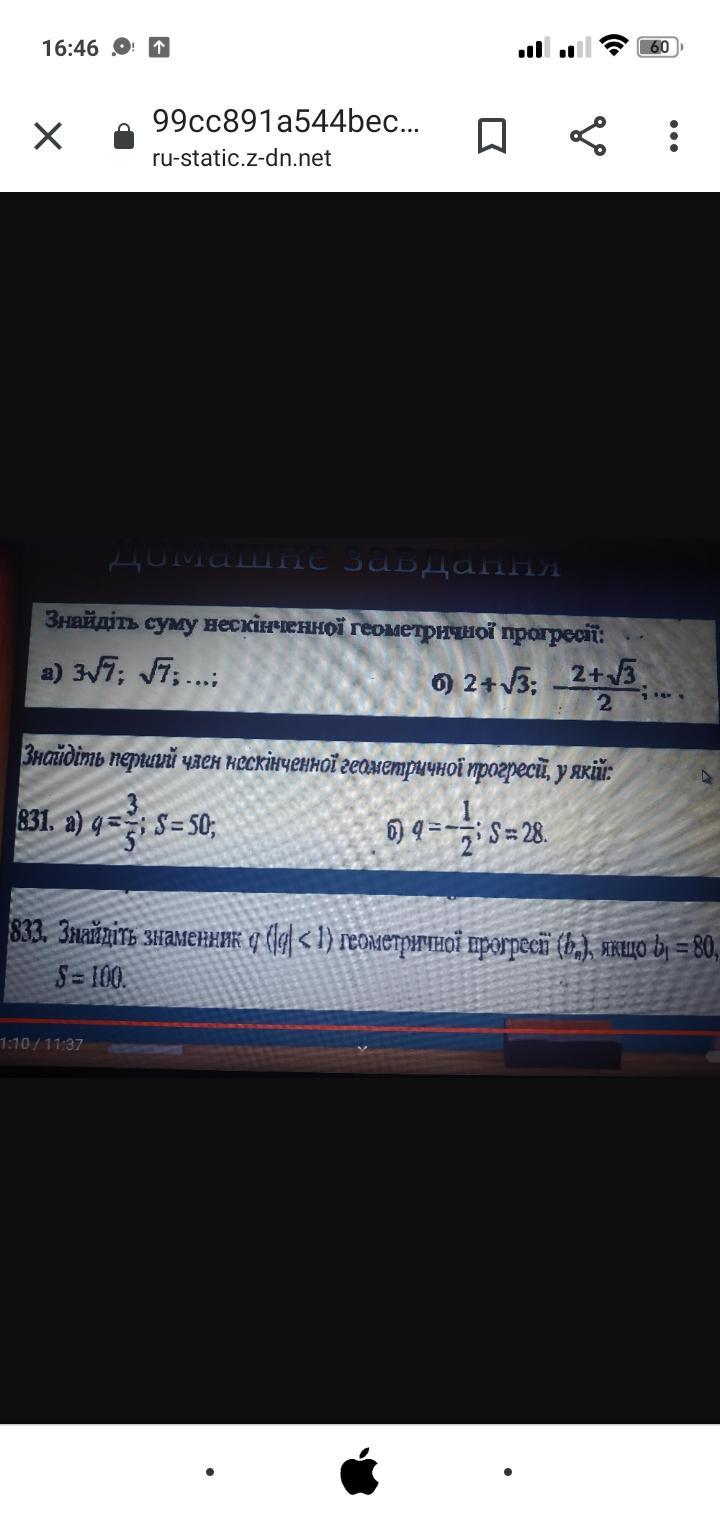
Відповідь: формула безкінечної спадної геометричної прогресії -
S= b1/(1-q), де b1 - перший член геометричної прогресії, q -знаменник
1. q=(√7)/(3√7) =1/3 S=(3√7)/(1-1/3)=(3√7)/(2/3)=(9√7)/2=4,5√7
2. q = ( (2+√3)/2) / (2+√3) )= 1/2 S= (2+√3)/ (1-1/2)=(2+√3) / (1/2)= 4+2√3
S= b1/(1-q), де b1 - перший член геометричної прогресії, q -знаменник
1. q=(√7)/(3√7) =1/3 S=(3√7)/(1-1/3)=(3√7)/(2/3)=(9√7)/2=4,5√7
2. q = ( (2+√3)/2) / (2+√3) )= 1/2 S= (2+√3)/ (1-1/2)=(2+√3) / (1/2)= 4+2√3
2 і 3 хто хоче хай пише, я нічого не бачу
Ответы
Автор ответа:
3
Спасибо огромное,напиши что бы я тебе кинула 40 б.
Похожие вопросы
Предмет: Русский язык,
автор: arinalyamzina2
Предмет: Математика,
автор: nikabalayankbp
Предмет: Математика,
автор: uribasik
Предмет: Физика,
автор: bboikov61