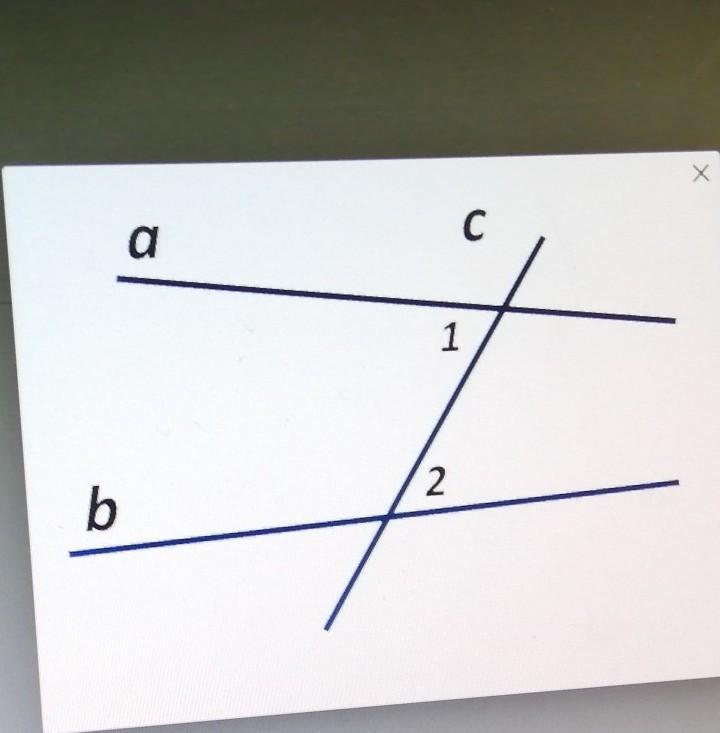
Углы 1 и 2 являются внутренними накрест лежащими при прямых a и b и секущей c.Угол 1 равен 67 градусов, а угол 2 равен 55 градусов. На сколько градусов нужно увеличить меньший угол, чтобы прямые a и b стали параллельными? В ответ впишите только цифры
Ответы
Ответ:
На 12° градусов нужно увеличить меньший угол, чтобы прямые a и b стали параллельными.
Объяснение:
Дано:
на рисунке прямые a и b пересечены прямой c; ∠1 и ∠2 внутренние накрест лежащие углы; ∠1 = 67°; ∠2 = 55°.
Найти:
на сколько градусов нужно увеличить меньший угол, чтобы прямые a и b стали параллельными?
Чтобы ответить на этот вопрос воспользуемся теоремой:
Признак параллельности прямых: если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
Прямая a будет параллельна прямой b, если накрест лежащие углы ∠1 и ∠2 будут равны.
По условию ∠1 = 67°; ∠2 = 55°. Разность между ними 67° - 55° = 12°.
Значит, если меньший угол увеличить на 12°, то выполнится условие a║b.
Таким образом, меньший ∠2 нужно увеличить на 12°.