Question

Обясните пожалуйста как ее решить!!!!!
3 точки А, яка не належить колу, проведено до кола дотичну і січну. Відстань від точки А до точки дотику дорівнює 12 см, а до одніеї з точок перетину січної з колом дорівнює 24 см. Знайдіть радіус кола, якщо січна віддалена від його центра на 12 см.

Answer 1

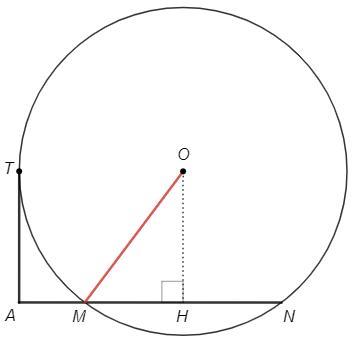
Из точки А, не лежащей на окружности, проведены к окружности касательная и секущая.  Расстояние от А до точки касания 12 см. Расстояние от A до одной из точек пересечения секущей с окружностью 24 см.  Найдите радиус окружности, если секущая удалена от центра на 12 см.

В сантиметрах

По теореме о касательной и секущей

AT^2 =AN*AM => 12^2 =24*AM => AM =144/24 =6

MN =AN-AM =24-6 =18

Расстояние от точки до прямой - длина перпендикуляра.

OH⊥AN, OH=12

Перпендикуляр из центра к хорде делит ее пополам.

MH =MN/2 =9

По теореме Пифагора

OM =√(OH^2 +MH^2) =15 (см)