Предмет: Геометрия,
автор: vi4147782
подобны ли треугольники?
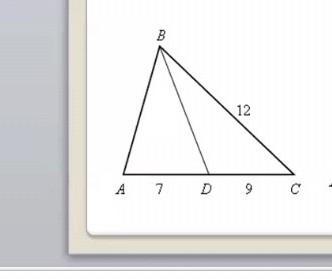
AD=7см
DC=9см
BC= 12см
Приложения:
Ответы
Автор ответа:
4
Ответ:
ΔBDC подобен ΔABC
Объяснение:
Рассмотрим треугольники BDC и ABC:
- ∠С - общий угол
- BC/AC=12/16=3/4
- DC/BC=9/12=3/4
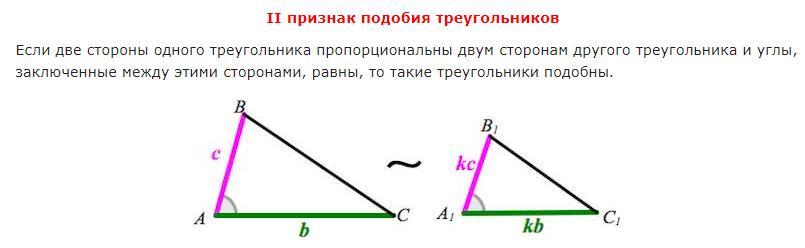
II признак подобия треугольников:
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
Значит, треугольники BDC и ABC подобны.
Приложения:
Автор ответа:
0
Ответ:
ΔАВС подобен ΔBDC
Объяснение:
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключённые между этими сторонами равны, то такие треугольники подобны. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключённые между этими сторонами равны, то такие треугольники подобны. (Второй признак подобия).
Рассмотрим ΔАВС и ΔBDC.
∠С у них общий.
Рассмотрим пропорциональность сторон треугольников, прилегающих к этому углу (расположим их в порядке возрастания):
ΔАВС: ВС=12см, АС= AD+DC=7+9=16cм
ΔBDC: DC=9 см, ВС = 12 см
Так как прилегающие стороны у этих треугольников пропорциональны, то ΔАВС подобен ΔBDC согласно второму признаку подобия.
Похожие вопросы
Предмет: Математика,
автор: sasha13022
Предмет: География,
автор: arinaasulova
Предмет: Литература,
автор: mronoprien
Предмет: История,
автор: ллпмтп
Предмет: История,
автор: hepoxet