Предмет: Алгебра,
автор: Mixtit
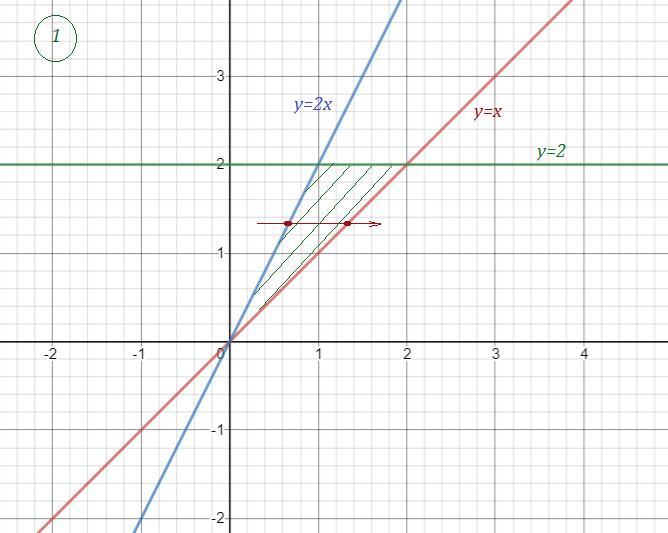
Вычислить двойной интеграл
Слева первое задание
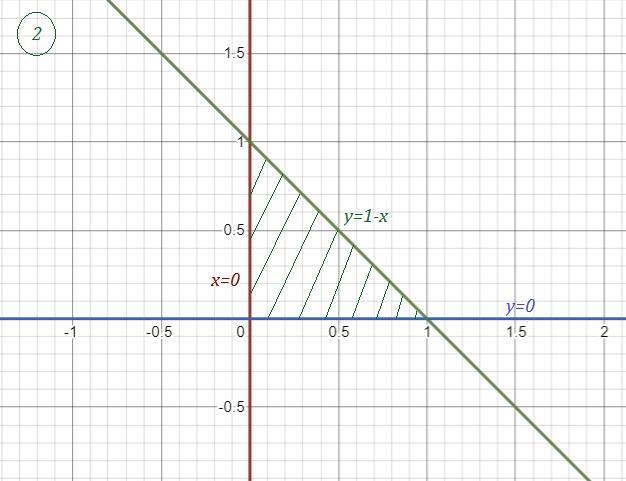
Справа второе задание
Приложения:

Ответы
Автор ответа:
0
Приложения:
Mixtit:
Спасибо конечно, но в прошлый раз вы мне выполнили эту же задачу неправильно
и что ?
Похожие вопросы
Предмет: Русский язык,
автор: drmir0608
Предмет: Русский язык,
автор: Белка1995847614
Предмет: Информатика,
автор: Мария06312
Предмет: История,
автор: GirlDemoness
Предмет: Алгебра,
автор: Artemisop