Предмет: Геометрия,
автор: sevaa456
Дана окружность, центр которой лежит на стороне AC треугольника ABC. Определи вид угла ∠B.
Радиус окружности равен 20.5, сторона AB равна 9. Найди сторону BC этого треугольника и определи вид одного из углов.

Рис. 1. Окружность
Ответ:
1. ∠B —
.
Варианты ответов:
прямой
острый
тупой
2. Сторона BC равна .
Ответы
Автор ответа:
1
Ответ:
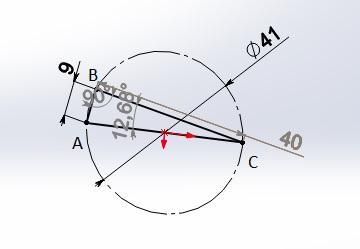
1. ∠в=90° прямой
2. BC =40
Объяснение:
sin∠С=AB/2r=9/41
∠С=12,68°
Приложения:
Автор ответа:
2
Ответ:
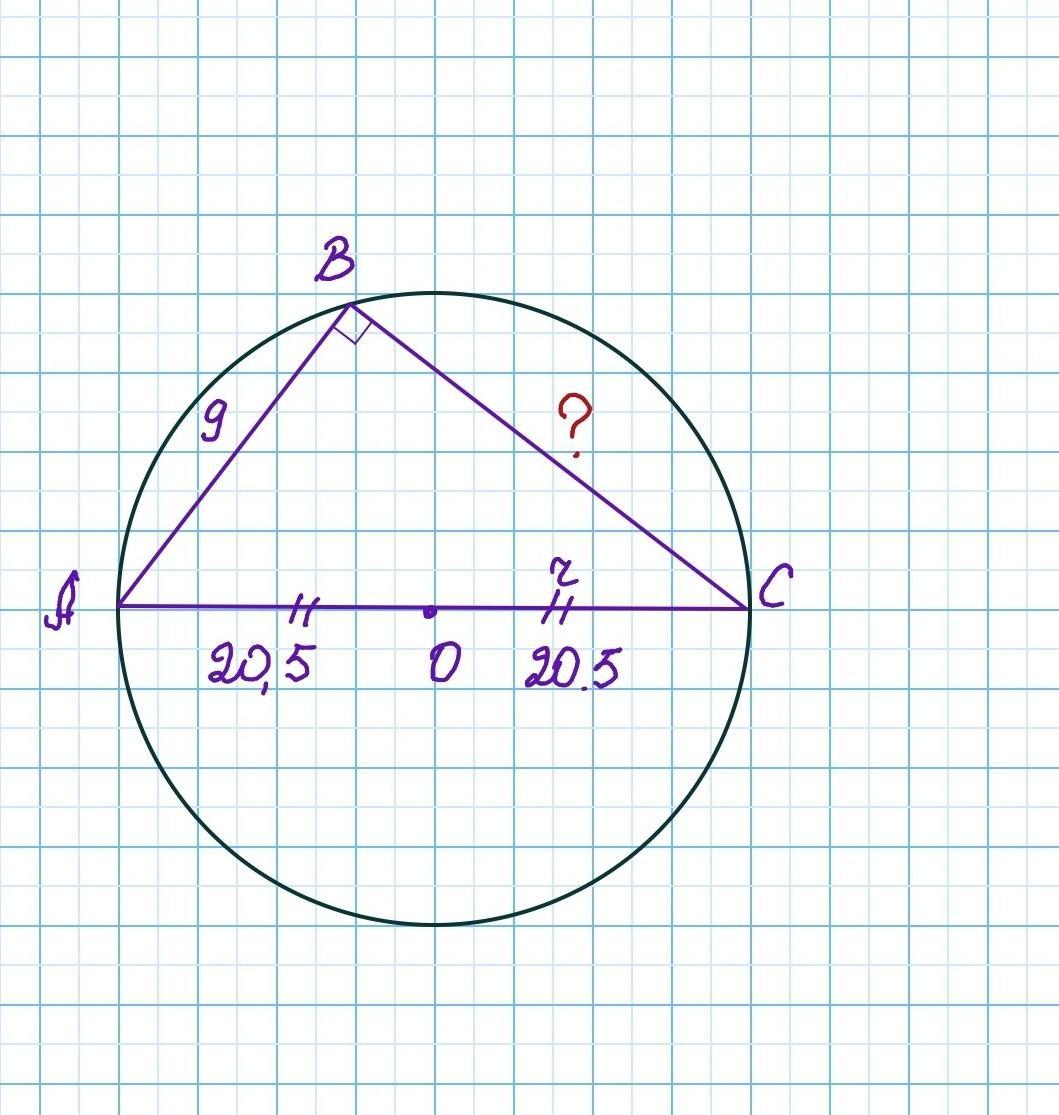
1. ∠B — прямой
2. Сторона BC равна 40 ед.
Объяснение:
1. Если центр описанной около треугольника окружности лежит на стороне треугольника, то этот треугольник — прямоугольный.
Сторона, на которой лежит центр описанной окружности, является гипотенузой.
Доказательство: AС — хорда проходящая через центр окружности => AС — диаметр. Так как вписанные углы, опирающиеся на диаметр — прямые, то ∠ABС=90º.
Треугольник ABC — прямоугольный, AС — гипотенуза.
2. Так как АС - диаметр, то АС=2×r=2×20,5=41
В прямоугольном треугольнике по теореме Пифагора найдём катет ВС:
Приложения:
Похожие вопросы
Предмет: Физика,
автор: Димон11111111111111
Предмет: Английский язык,
автор: shynargulbaibo
Предмет: Биология,
автор: proz2016
Предмет: Математика,
автор: Аноним
Предмет: Музыка,
автор: умница646