Предмет: Алгебра,
автор: timanematov472
Это срочно,пожалуйчта помогите.Ответ с решением
Приложения:

Miroslava227:
4 задание, буква б, там пределы 0 и 4?
очень мелко написано
Там пределы 0 и 4,да
Ответы
Автор ответа:
1
Ответ:
решение на фотографии
в 4б проверьте пределы, очень мелко написано
Приложения:
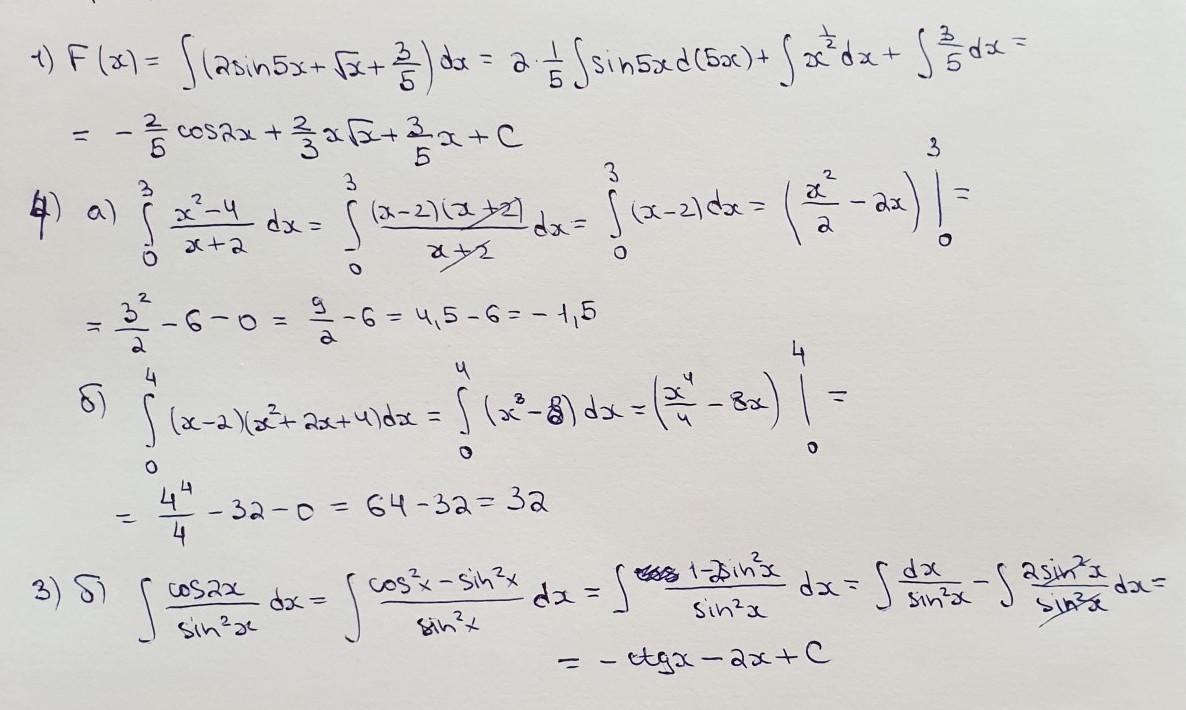
Автор ответа:
0
Похожие вопросы
Предмет: Алгебра,
автор: кристинатимченко
Предмет: Алгебра,
автор: luba2111
Предмет: Русский язык,
автор: abiankin
Предмет: Физика,
автор: kirill925