Question

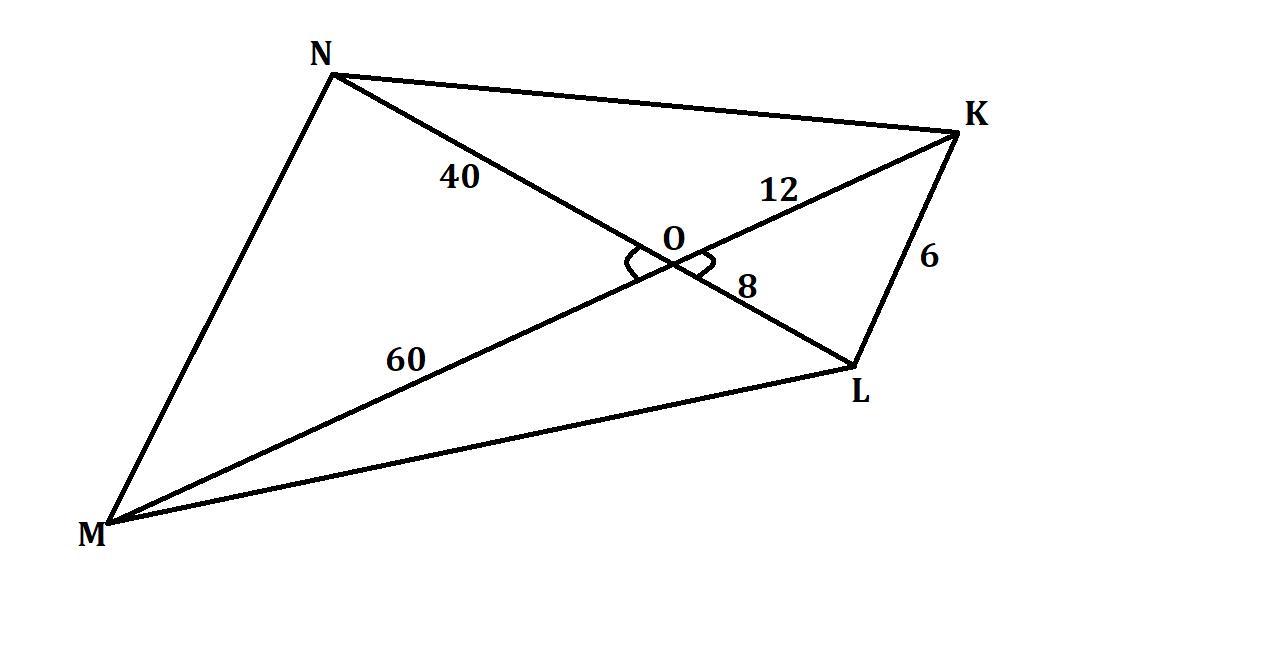
Диагонали выпуклого четырёхугольника KLMN пересекаются в точке O. Найдите MN, если OK=12, OL=8, KL=6, OM=60, ON=40

Answer 1

Ответ:

30

Объяснение:

Рассмотрим $\triangle MON$ и $\triangle KOL$:

$\dfrac{OL}{ON} =\dfrac{8}{40} =\dfrac{1}{5}$,  $\dfrac{OK}{OM} = \dfrac{12}{60} = \dfrac{1}{5}$ $\Rightarrow \dfrac{OL}{ON} = \dfrac{OK}{OM}= \dfrac{1}{5}$

$\angle NOM = \angle LOK$, по свойству вертикальных углов

$\Rightarrow \triangle MON \sim \triangle KOL$, по 2 признаку подобия треугольников (по 2 пропорциональным сторонам и углу между ними)

• В подобных треугольниках сходственные стороны пропорциональны.

$\Rightarrow \dfrac{OL}{ON} = \dfrac{OK}{OM}=\dfrac{KL}{MN} =\dfrac{1}{5}$

$\dfrac{KL}{MN} = \dfrac{1}{5}$

$\dfrac{6}{MN} = \dfrac{1}{5}$

• Свойство пропорции: произведение крайних членов равно произведению средних.

$MN \cdot 1 = 6 \cdot 5$

$MN = 30$