Предмет: Алгебра,
автор: kingcrest
С подробным решением!
Приложения:
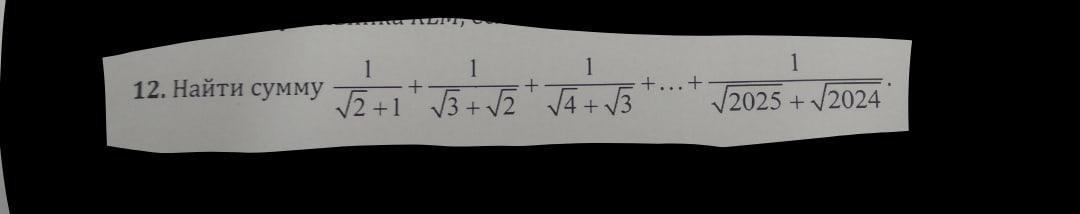
Ответы
Автор ответа:
2
Похожие вопросы
Предмет: Литература,
автор: lerokvalerok
Предмет: Математика,
автор: кошка1234567890
Предмет: Русский язык,
автор: lagoda74
Предмет: Геометрия,
автор: muhammedsadukooutfuc
Предмет: Геометрия,
автор: София944