Предмет: Алгебра,
автор: noname324533
5.3. Преобразуйте выражение:
1
1)
5)
» (.
у
+
4
3
2
2
1
6) 12 – т
3
т +1
2) [b+
3
n
п
3)
7) | 5т -
;
а
2
2
4)
;
| с.
8) 9р
т
Приложения:
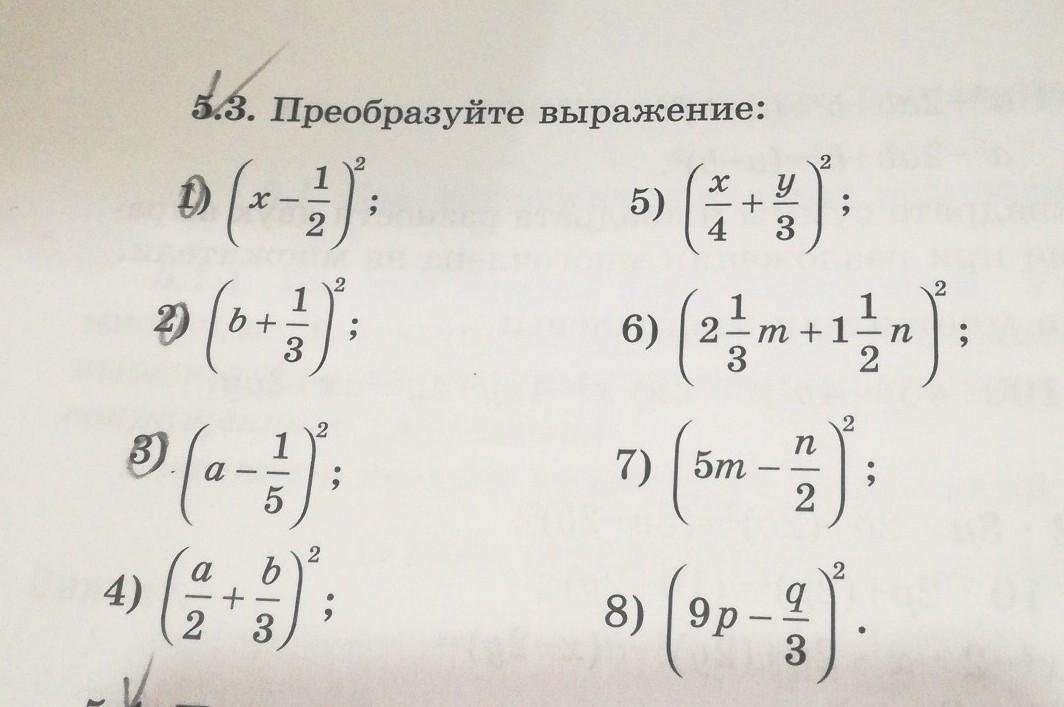
Ответы
Автор ответа:
18
Объяснение:
Воспользуемся формулами сокращенного умножения
Похожие вопросы
Предмет: Химия,
автор: valyamina
Предмет: Русский язык,
автор: макслайкер
Предмет: История,
автор: legushkamarb
Предмет: Математика,
автор: мттслалаьвьбвбвбввв