Предмет: Алгебра,
автор: reallyrodion2
Задай формулой квадратичную функцию вида y = ax2 + bx + c, если график функции проходит через точку (–2; 0), а при x = 2 значение функции y = –32 – наименьшее.
Приложения:
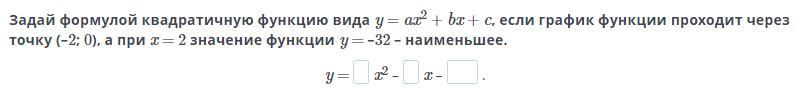
keiwa200067:
y=x^2-2x-3
y = 2x² - 8x - 24
y=x^2-2X-3
Для тех у кого y=x^2-2X-3,
вы подставьте х= 2 , у вас действительно получится -32 ????
вы подставьте х= 2 , у вас действительно получится -32 ????
Ответы
Автор ответа:
83
Ответ:
y = 2x² - 8x - 24
Объяснение:
Подставим x = 2, y = -32:
-32 = 4a + 2b + c (*)
Подставим x = -2, y = 0:
0 = 4a - 2b + c |(-1)
0 = -4a + 2b - c (**)
Складываем уравнения (*) и (**):
-32 = 4b => b = -8
При x = 2, y = -32 — наименьшее или вершина параболы
x(вершина) = 2 = -b/2a => a = -b/2x(вершина) = -(-8)/2*2 = 2
0 = 2*4 - 2*(-8) + c
c = -24
Уравнение имеет вид:
y = 2x² - 8x - 24
ответ 22
Ответ:y=-2x^2-4x+48
Это правильный
Спасибо
()
И так уже и не то
И не знаю что это такое но вы ведёт себя плохо
Спасибо но не надо
Зачем вы путаете людей?? ОТВЕТ ПРАВИЛЬНЫЙ! ЗАЧЕМ ВЫ ВСЯКУЮ ДИЧЬ ПИШЕТЕ?
Похожие вопросы
Предмет: Физика,
автор: wladik001
Предмет: Русский язык,
автор: nastya20124
Предмет: Английский язык,
автор: e200605
Предмет: Математика,
автор: 0206dantur
Предмет: Математика,
автор: Nastya222222999