Question

Стороны оснований правильной усеченной треугольной пирамиды равны 2 и 4 см, угол наклона боковых граней к основанию равен 60 градусам. Найдите объём пирамиды.

ОТДАМ ВСЕ 35 БАЛЛОВ, КОТОРЫЕ ЕСТЬ!!!!!!!!!

Answer 1

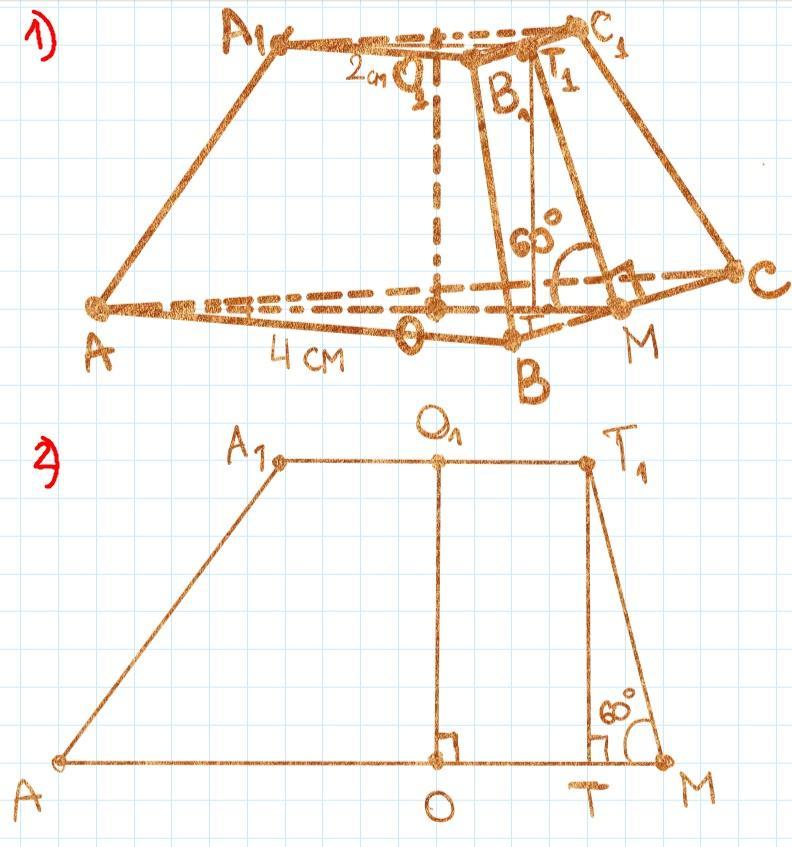
Смотрим 1-й чертеж!

Воспользуемся формулой объема усеченной пирамиды:

V = ⅓·h·(S₁+√(S₁·S₂)+S₂), где h - высота усеченной пирамиды, S₁ - площадь нижнего основания, S₂ - площадь верхнего основания

1) Находим площади оснований по формуле площади равностороннего треугольника:

S = ¼· a²·√3, где a - сторона правильного треугольника.

S₁ = ¼ · 4²·√3 = 4√3 см²

S₂ = ¼ · 2²·√3 = √3 см²

Смотрим 2-й чертеж!

2) Ищем h

O₁T₁ = ⅓ A₁T₁; A₁T₁ = 0,5√3 · 2 = √3 см ⇒ O₁T₁ = ⅓√3 см

OM = ⅓ AM; AM = 0,5√3 · 4 = 2√3 см ⇒ OM = ⅔√3 см

TM = OM - O₁T₁ = ⅓√3 см

В ΔTT₁M: ∠T = 90°; ∠M = 60°; tg 60° = TT₁ ÷ TM ⇒ TT₁ = ⅓√3 · √3 = 1 см

⇒ h = 1 см

3) Собираем все вместе:

V = ⅓·h·(S₁+√(S₁·S₂)+S₂) = ⅓ · 1 · (4√3 + √(4√3·√3) + √3) = ⅓ 7√3 см³ = 7÷√3 см³