Предмет: Алгебра,
автор: danbert444
помогите алгебра 10 класс 25 балов
Приложения:
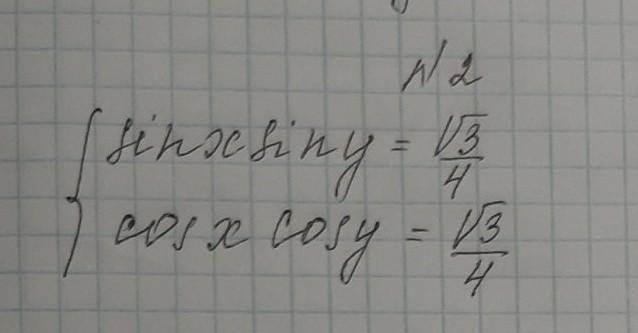
Ответы
Автор ответа:
1
сложим уравнения
1) x=y+π/6
1.1 ) 2y+π/6= π/2+2πn
1.2) 2y+π/6= -π/2+2πn
ответом на 1 случай (π/3+2πn; π/6+2πn) или (-π/3+2πn; -π/3+2πn)
2) x= y-π/6
решаем аналогично
2.1) 2y-π/6=π/2+2πn
2.2) 2y-π/6= -π/2+2πn
ответом на 2 случай (π/6+2пn; π/3+2πn) или (-π/3+2πn; -π/6+2πn)
Похожие вопросы
Предмет: Математика,
автор: MaruWorI13
Предмет: Математика,
автор: pluev
Предмет: Английский язык,
автор: elenbystr
Предмет: Биология,
автор: konslida