Предмет: Математика,
автор: dimafoks1996
С помощью логарифмического дифференцирования вычислите производные данных функций:
Приложения:
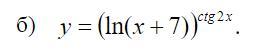
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Химия,
автор: jlhat14
Предмет: Математика,
автор: Danil200212
Предмет: Другие предметы,
автор: лерочка0114
Предмет: Геометрия,
автор: Kiladze57