Предмет: Математика,
автор: glebokkamyshkin
С помощью логарифмического дифференцирования вычислите производные данной функции
Приложения:
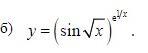
Ответы
Автор ответа:
0
Ответ:
egma228:
поможешь с контрольной?
даю 150 балов
здравствуйте, помогите мне по математике пожалуйста
здравствуйте помогите мне пожалуйста по математике.
Похожие вопросы
Предмет: Информатика,
автор: trexxr
Предмет: Химия,
автор: ashotavagyan9
Предмет: Математика,
автор: arinapod
Предмет: Математика,
автор: tat2911