Предмет: Алгебра,
автор: Mixtit
Вычислить криволинейный интеграл
Приложения:
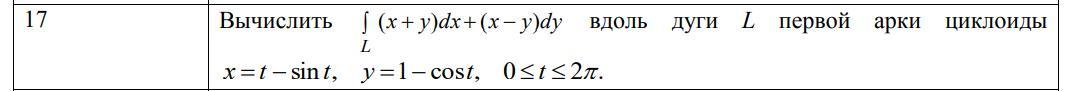
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: История,
автор: emilabrekov
Предмет: География,
автор: FinestVlad
Предмет: Математика,
автор: dauren157
Предмет: Химия,
автор: Аноним