Предмет: Математика,
автор: arokai1233
Найти синус косинус и тангенс. Дан котангенс бета = 2
Приложения:
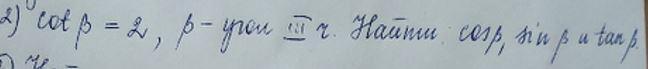
Ответы
Автор ответа:
0
Ответ:
угол принадлежит 3 четверти, значит cosB и sinB отрицательные, tgB - положительный.
Воспользуемся формулой:
Похожие вопросы
Предмет: Русский язык,
автор: 620841
Предмет: Русский язык,
автор: ayauomarbekova
Предмет: Математика,
автор: YanaGerz
Предмет: Литература,
автор: ladylandish
Предмет: Математика,
автор: disuwun