Предмет: Алгебра,
автор: Аноним
Алгебра.
Задание 321.
Приложения:
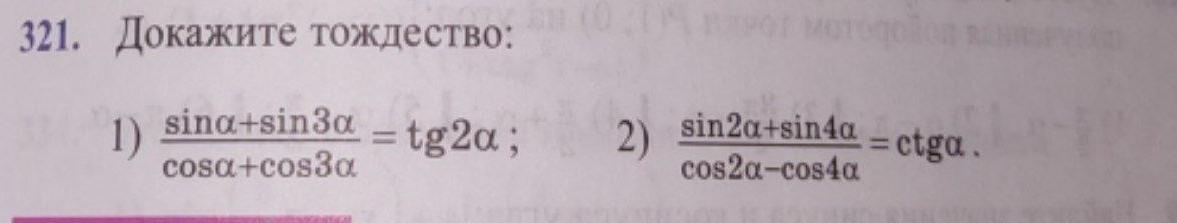
Ответы
Автор ответа:
2
Universalka:
Пожалуйста
Похожие вопросы
Предмет: История,
автор: Аноним
Предмет: Русский язык,
автор: natuciktabolic1
Предмет: Другие предметы,
автор: nazar77771
Предмет: Химия,
автор: irka110
Предмет: Литература,
автор: Cooldude500