В пирамиде SABC SB = 4 см, SA = 3 см, SC = 7см, AC = √58 см, BC = √65 см, угол ASB = 30°. Найдите объём пирамиды. Буду признательна. С рисунком, пожалуйста.
Ответы
Пусть основание пирамиды - грань АВС.
Решение удалось только с применением аналитической геометрии.
Находим длину стороны АВ по теореме косинусов.
AB = √(BS2 + AS2- 2*BS*AS*cos(BSA)) =
= √(42 + 32- 2*4*3*cos(30°)) = √(16 + 9 - 24*(√3/2)) =
= √(25 - 12√3) = 2,0531.
Пирамиду поместим в систему координат: точкой А(0; 0;0) в начало, точкой С(√58; 0; 0) - по оси Ох.
Для определения положения проекции вершины пирамиды точки S на основание (это точка So) к сторонам треугольника АВС наложим развёртки боковых граней.
Точка So находится на пересечении перпендикуляров из наложенных точек S к сторонам треугольника АВС.
По теореме косинусов определяем углы треугольника АВС и координаты точки В.
cosA = ((√58)² + (√(25-12√3))² - (√65)²)/(2*√58*√(25 - 12√3)) =
= (-2,784609691/31,27252071) = -0,089043.
A = arc cos(-0,089043) = 1,659958 радиан или 95,108574 градуса.
Находим координаты точки В:
х(В) = AB*cosA = √(25 - 12√3)*( -0,089043) = -0,182819.
y(B) = AB*sinA = √(25 - 12√3)*√(1-(-0,089043)²) = √(25 - 12√3)*0,996028 = .
= 2,044986.
По координатам точек А и В составляем уравнение стороны АВ в плоскости АВС (с учётом, что координаты вектора АВ численно равны координатам точки В):
(x/(-0,182819) = (y/2,044986) или в общем виде 2,044968x + 0,182819y = 0.
Находим уравнения перпендикуляров к сторонам АВ и АС из наложенных точек S.
Для этого решаем треугольники боковых граней ABS и ACS и находим проекции ребра AS на стороны АВ и АС.
AS₁ AS₂
-0,678134 1,181758.
С учётом углов наклона к осям отрезков AS₁и AS₂ находим координаты точек S₁ и S₂.
x(S₁) = AS₁*cos(BAC) = -0,678134*(-0,089043) = 0,06038,
y(S₁) = AS₁*sin(BAC) = -0,678134*0,996028 = -0,67544,
x(S2) = 1,181758,
y(S2) = 0.
По ним находим уравнения перпендикуляров и точку их пересечения So
Уравнение S₁So: -0,182819 x + 2,044986 y + C = 0,
Подставляем координаты точки S₁ и определяем С = -1,392305:
Уравнение S1S0
0,182819x - 2,044986y - 1,392305 = 0 или с угловым коэффициентом
y = 0,0894x - 0,680838.
Уравнение S2S0: x = 1,181758
или с угловым коэффициентом y = -0,0626 x + 3,632101.
Подставим сюда х точки S₂ и получаем координаты проекции точки S на АВС.
координаты So:
х у
1,181758 -0,575191
По Пифагору находим величину проекции AS на АВС:
АSo = 1,314305.
Отсюда определяем высоту пирамиды:
H = SSo = √(3² - 1,314305²) = 2,696777.
Площадь основания АВС равна:
S(ABC) = 7,7871 кв.ед.
Отсюда объём пирамиды равен:
V = (1/3)SoH = (1/3)*7,7871*2,696777 = 7 куб.ед.
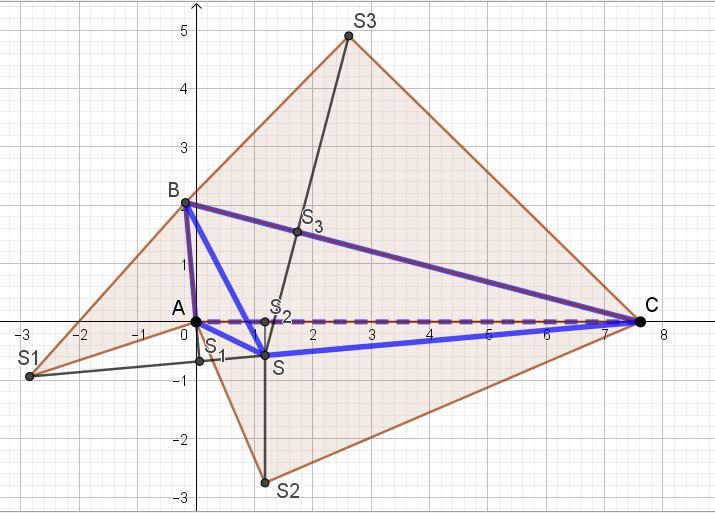
4^2 +7^2 =65 => BSC=90
SC⊥(ASB)