Предмет: Геометрия,
автор: mashamaltheva
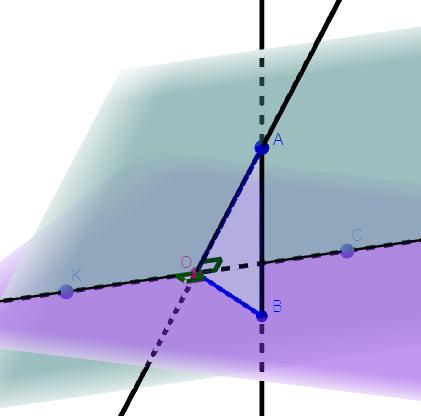
На одній із граней двогранного кута, величина якого дорівнює 45°, позначили точку А. Відстань від точки А до ребра двогранного кута дорівнює 10 см. Знайдіть відстань від точки А до другої грані двогранного кута
Ответы
Автор ответа:
16
Ответ:
см
Объяснение:
Дано: ∠AOB = 45°, AO ⊥ KC, OB ⊥ KC, AO = 10 см, AB ⊥ BO
Знайти: AB - ?
Розв'язання: Так як за умовою AO ⊥ KC, OB ⊥ KC, то кут ∠AOB - лінійний кут двохгранного кута. Так як за умовою AB ⊥ BO, то трикутник ΔAOB - прямокутний. За означенням синуса у прямокутному трикутнику:
см.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: рррррррит
Предмет: Русский язык,
автор: ira45335
Предмет: Алгебра,
автор: aruka99
Предмет: Геометрия,
автор: AlmatLucky