Question

ПОМОГИТЕ СРОЧНО!!!
"Решение треугольников, теорема синусов" найти x и y​

Answer 1

Ответ:

Неизвестные элементы треугольников:

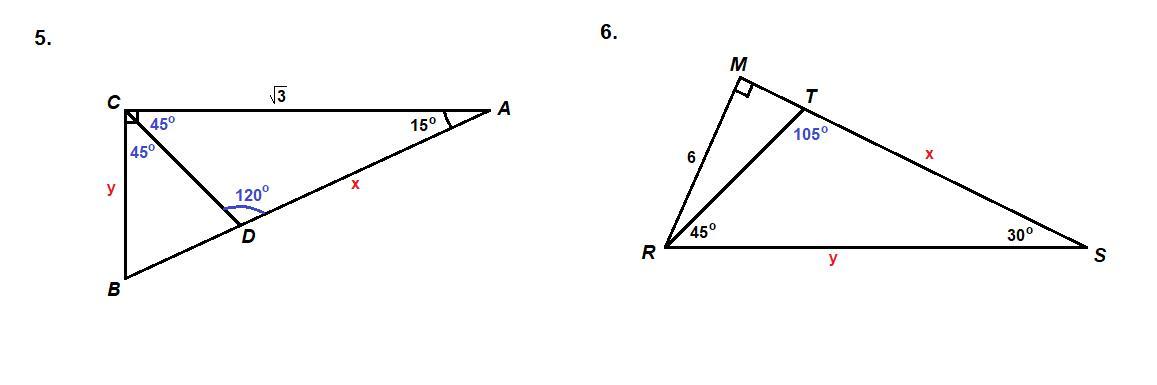
5.

$x=\sqrt{2}$

$y=2\sqrt{3}-3\approx 0,46$

6.

$x=12(\sqrt{3}-1)\approx 8,7$

у = 12

Объяснение:

5.

CD - биссектриса прямого угла, значит

∠ACD = 0,5 ∠ ABC = 45°

Сумма углов треугольника равна 180°.

ΔACD:

∠ADC = 180° - (15° + 45°) = 180° - 60° = 120°

По теореме синусов:

$\dfrac{AD}{\sin\angle ACD}=\dfrac{AC}{\sin\angle ADC}$

$\dfrac{x}{\sin 45^\circ}=\dfrac{\sqrt{3}}{\sin 120^\circ}$

$x=\dfrac{\sqrt{3}\cdot \sin 45^\circ}{\sin 120^\circ}$

$\sin 45^\circ =\dfrac{\sqrt{2}}{2}\\\sin 120^\circ =\dfrac{\sqrt{3}}{2}$

$\boldsymbol{x}=\sqrt{3}\cdot \dfrac{\sqrt{2}}{2}\cdot \dfrac{2}{\sqrt{3}}\boldsymbol{=\sqrt{2}}$

Из прямоугольного треугольника АВС:

$tg \angle A=\dfrac{BC}{AC}$

$tg\; 15^\circ=\dfrac{y}{\sqrt{3}}$

$tg\; 15^\circ\approx 0,2679$  (с помощью таблицы)

$y=\sqrt{3}\cdot tg\; 15^\circ\approx 1,7\cdot 0,2679$

$\boldsymbol{y\approx 0,46}$

______________________________________

Если уже изучали тригонометрические формулы (тангенс половинного аргумента), то можно вычислить у так:

$tg\; 15^\circ =\dfrac{1-\cos 30^\circ}{\sin30^\circ}$

$tg\; 15^\circ =\dfrac{1-\dfrac{\sqrt{3}}{2}}{\dfrac{1}{2}}=2\cdot \left(1-\dfrac{\sqrt{3}}{2}\right)=2-\sqrt{3}$

$\boldsymbol{y}=\sqrt{3}\cdot (2-\sqrt{3})\boldsymbol{=2\sqrt{3}-3}$

_______________________________________

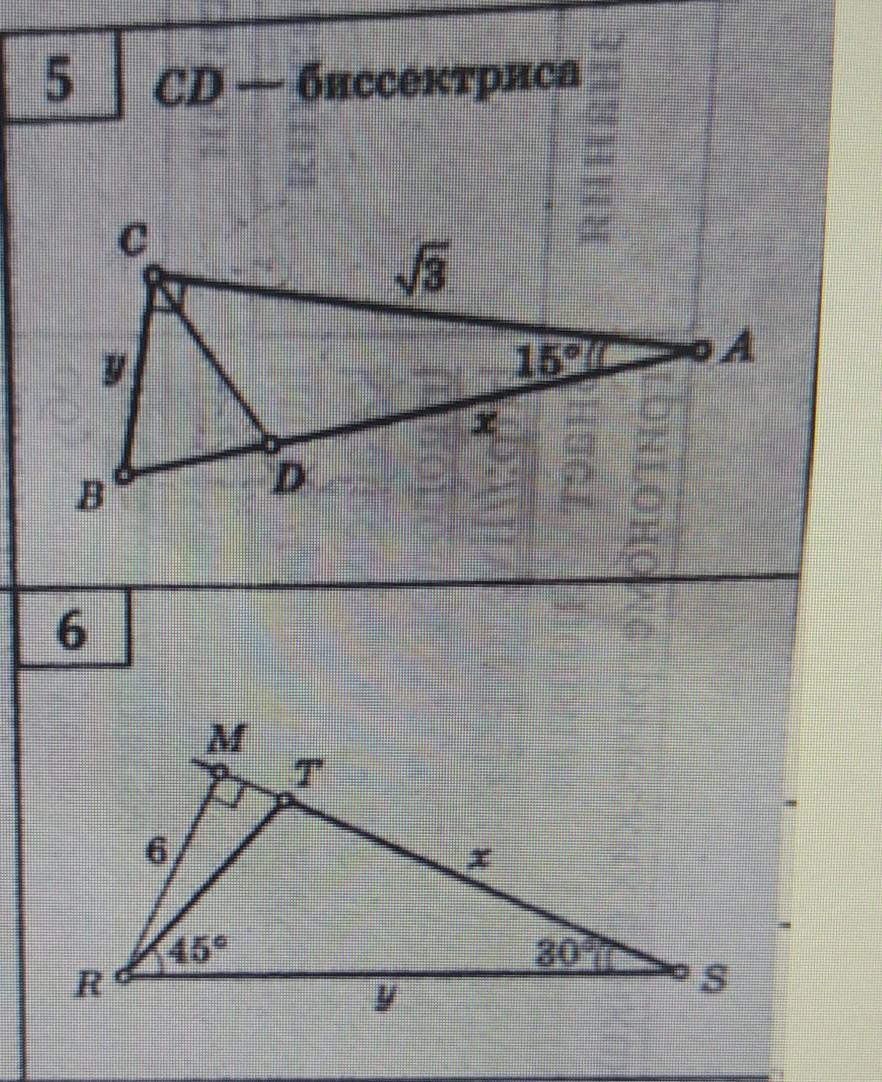
6.

В треугольнике RMS катет MR = 6 лежит против угла в 30°, значит он в два раза меньше гипотенузы.

y = RS = 2 · MR = 12

Из ΔRTS:

∠RTS = 180° - (45° + 30°) = 105°

По теореме синусов:

$\dfrac{TS}{\sin\angle TRS}=\dfrac{RS}{\sin\angle RTS}$

$\dfrac{x}{\sin 45^\circ}=\dfrac{12}{\sin 105^\circ}$

$x=\dfrac{12\cdot \sin 45^\circ}{\sin 105^\circ}$

$\sin 105^\circ =\sin(180^\circ -75^\circ)=\sin 75^\circ\approx 0,9659$   (с помощью таблицы)

$x\approx 12\cdot \dfrac{\sqrt{2}}{2}: 0,9659$

$x\approx 6\cdot 1,4: 0,9659$

$\boldsymbol{x\approx 8,7}$

_______________________________________

Если уже изучали тригонометрические формулы (синус суммы), то можно вычислить х так:

$\sin 105^\circ =\sin(60^\circ + 45^\circ)=\sin60^\circ\cos45^\circ+\cos 60^\circ\sin 45^\circ$

$\sin 105^\circ=\dfrac{\sqrt{3}}{2}\cdot \dfrac{\sqrt{2}}{2}+\dfrac{1}{2}\cdot \dfrac{\sqrt{2}}{2}=$

$=\dfrac{\sqrt{6}}{4}+\dfrac{\sqrt{2}}{4}=\dfrac{\sqrt{6}+\sqrt{2}}{4}=\dfrac{\sqrt{2}(\sqrt{3}+1)}{4}$

$x=12\cdot \dfrac{\sqrt{2}}{2}\cdot \dfrac{4}{\sqrt{2}(\sqrt{3}+1)}=\dfrac{24}{\sqrt{3}+1}$

$\boldsymbol{x}=\dfrac{24(\sqrt{3}-1)}{3-1}\boldsymbol{=12(\sqrt{3}-1)}$