Предмет: Математика,
автор: raevskysvyatoslav
Предел функции с развернутым решением
Приложения:
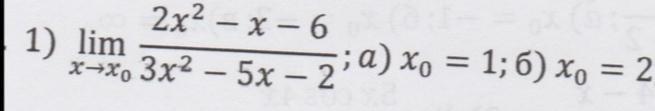
Ответы
Автор ответа:
1
1)
a)
б)
Аноним:
у меня ошибка в б) там предел равен 1.
Автор ответа:
0
Ответ:
Пошаговое объяснение:
поскольку и числитель и знаменатель обращаются в нуль при x=2, то 2 – корень обоих многочленов, а значит, каждый из них разлагается на множители, одним из которых будет (x - 2)
находим корни и пользуемся формулой ах² + bx + c = a(x-x₁)(x-x₂)
2x² -x =6 = 2(x-2)(x+1.5)
3x^2 -5x -2 = 3(x-2)(x+1/3)
тогда предел выглядит так
Похожие вопросы
Предмет: Алгебра,
автор: KateRav
Предмет: Математика,
автор: lomalena32
Предмет: Английский язык,
автор: marinasuper
Предмет: Литература,
автор: Миленаlife
Предмет: Математика,
автор: Akif1982