Предмет: Алгебра,
автор: Mixtit
Прошу помогите с алгеброй
первое задание слева
второе задание справа
Приложения:

Ответы
Автор ответа:
1
Ответ:
Приложения:
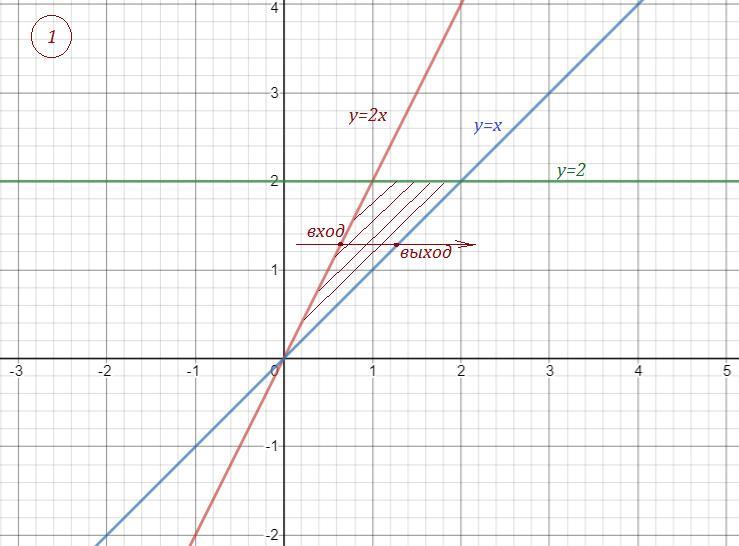
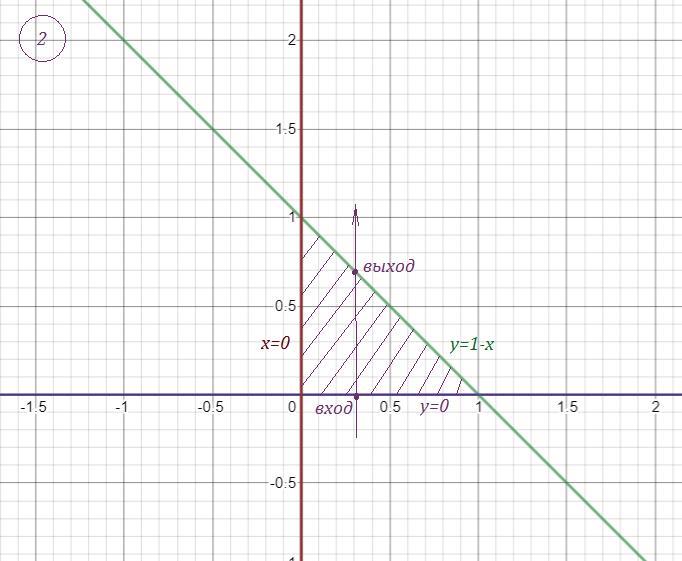
Mixtit:
Прошу помоги с моими задачами по алгебре
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: bogdanrumynskiy
Предмет: Математика,
автор: cirill2002
Предмет: Экономика,
автор: Аноним
Предмет: Математика,
автор: gricayukaleksa