Предмет: Математика,
автор: aa0268089
решить пределы пределы на фото
Приложения:
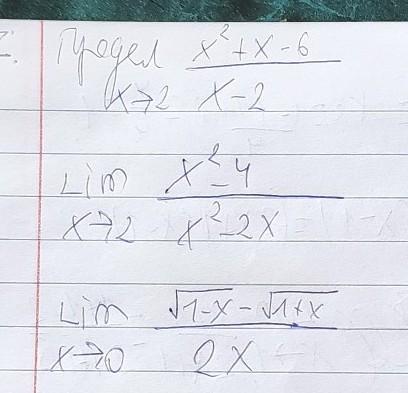
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Похожие вопросы
Предмет: Математика,
автор: degtereva1206
Предмет: Алгебра,
автор: harmanlucia
Предмет: Русский язык,
автор: kim123kim24
Предмет: Литература,
автор: svetlanalushch
Предмет: Геометрия,
автор: hadijat0807