Предмет: Алгебра,
автор: 24211626l
Сумма и разность кубов двух выражений. Урок 1
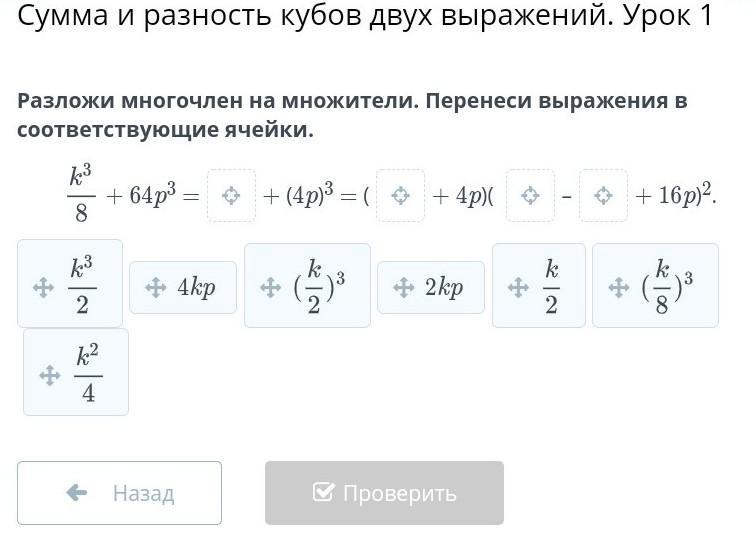
Разложи многочлен на множители. Перенеси выражения в соответствующие ячейки.
помогите пожалуйста
Приложения:
Ответы
Автор ответа:
2
Ответ:
Разложим многочлен на множители применив следующую формулу сокращённого умножения:
a³+b³ = (a+b)·(a²-a·b+b²).
Получим:
Значит, в первую пустую ячейку переносим
во вторую пустую ячейку переносим
в третью пустую ячейку переносим
в четвёртую пустую ячейку переносим
Похожие вопросы
Предмет: Геометрия,
автор: лана101
Предмет: Обществознание,
автор: Елизавета2305
Предмет: Английский язык,
автор: Maks771007
Предмет: География,
автор: denismakarenro