Надо решить через метод интервалов, буду очень благодарен

Ответы
Ответ: 2)х∈(-∞;1]∪[3;∞)
3)х∈(-∞;-1]∪[2;∞)
4)х∈[-1;2)
5) х∈(-8;-1)∪(1;2)
6) Y∈[0;4]
Пошаговое объяснение:
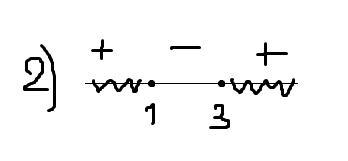
2)
-х²+4x-3≤0
поменяем знаки: x²-4x+3≥0
найдем нули: x²-4x+3≥0; D=4; x1=3 и x2=1
найдем интервалы(картинка): х∈(-∞;1]∪[3;∞)
3)
(х-2)(х+1)≥0
найдем нули:
x-2=0; x+1=0
x=2; x=-1
найдем интервалы (картинка): х∈(-∞;-1]∪[2;∞)
4)
(x+1)/(x-2)≤0
имеем дробь ⇒ исключаем нули знаменателя и ищем нули числителя:
х-2≠0 и х+1=0
получили две точки (одну выколотую) : х≠2 и х=-1
найдем интервалы (картинка): х∈[-1;2)
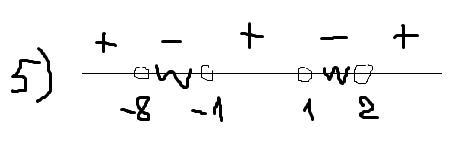
5)
(x²+6x-16)(x²-1)<0
приравниваем обе части к нулю:
x²+6x-16 = 0 и x²-1=0
D=100 x3=1 x4=-1
x1=-8 и x2=2
найдем интервалы(картинка): х∈(-8;-1)∪(1;2)
6) Область значений - то, что может принимать Y
смотрим на функцию - это точно парабола (дальше поймем, что она еще ограниченная и смещенная)
- функция стоит под корнем ⇒ должно выполняться условие Y≥0 (ограниченность)
- старший коэффициент отрицательный ⇒ ветви направлены вниз
- находим вершину по формуле x=-b/2a и получаем х=-2 (смещенность)
из этого следует, что парабола начинается по Y в точке Y(-2) = 4
и дальше она должна расти безгранично вниз, однако не забываем про условие Y≥0
⇒ Y∈[0;4]
-------------------------------------------------------------------------------------------------------
ПОИСК ИНТЕРВАЛОВ:
1) найденные точки располагаем на прямой и расставляем знаки в промежутках: подставляем число из промежутка в изначальный пример и смотрим, какого знака получается ответ. если отрицательного - промежуток отрицательный (аналогично с положительным значением)
2) смотрим на изначальное неравенство: строгое неравенство - все точки выколотые, нестрогое - точки принадлежат; больше нуля - выбираем в ответ положительные промежутки (меньше - отрицательные)