Предмет: Математика,
автор: georgefilin
Можете помочь пожалуйста за 45 баллов
Приложения:
pushpull:
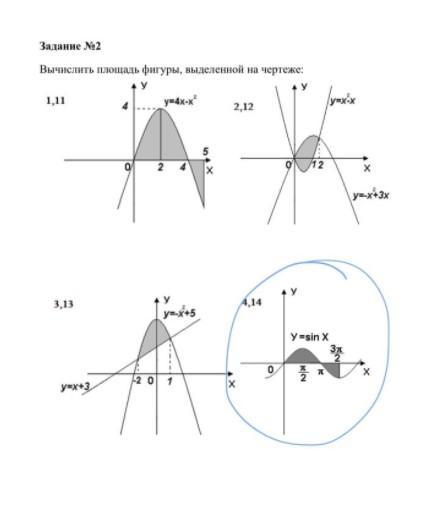
1.11 решила здесь https://znanija.com/task/41980585?answeringSource=feedPublic%2FhomePage%2F6
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
1.11 решила здесь https://znanija.com/task/41980585?answeringSource=feedPublic%2FhomePage%2F6
2.12
3.13
4.14
конечно, интегралы 1.11 и 4.14 можно было разбивать на 3 равноплощадных... но проще тупо взять в лоб целиком по площади. возьни меньше...
Похожие вопросы
Предмет: Математика,
автор: elenashiryaeva
Предмет: Математика,
автор: supermimimneka
Предмет: Биология,
автор: nelya1857
Предмет: Алгебра,
автор: kgourarioussam
Предмет: Алгебра,
автор: kgourarioussam