Предмет: Алгебра,
автор: neanimeshnik079
ДАЮ 35 баллов. Показательные неравенства.
пожалуйста решите задачу, и с объяснениями каждого шага(если не сложно)
Приложения:
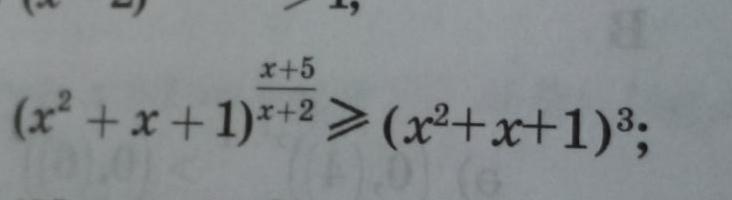
Ответы
Автор ответа:
2
Ответ:
рассмотрим два случая:
1) когда основания < 1 (знак меняется)
2) > 1, знак остаётся прежним
1.
пересекаем оба решения:
2.
пересекаем:
объединяем два решения:
Похожие вопросы
Предмет: Алгебра,
автор: bembio
Предмет: Математика,
автор: angelfrozen
Предмет: Английский язык,
автор: tinysa08
Предмет: Математика,
автор: 0984566413
Предмет: Алгебра,
автор: оксана749