Question

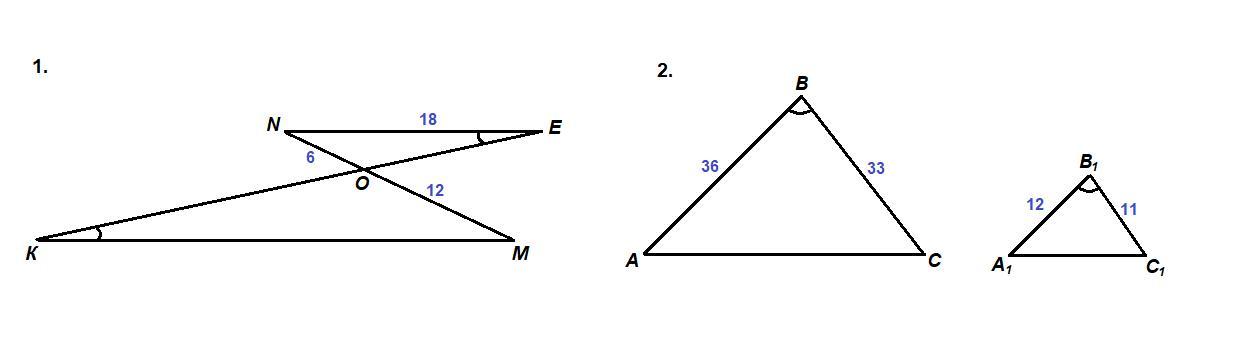
Отрезки KE и MN пересекаются в точке O так что отрезок KM параллелен отрезку NE докажите что треугольники KMO и NEO подобны найдите KM если ON=6см MO=12см NE=18см,

Докажите что треугольники ABC и A1B1C1 подобны, если угол B равен углу B1, AB=36см A1B1=12cm BC=33 cm B1C1=11 cm
с рисунком пжлста))​

Answer 1

Ответ:

1. КМ = 36 см

Объяснение:

1.

∠ОКМ = ∠OEN как накрест лежащие при пересечении параллельных прямых КМ и NE секущей КЕ,

∠КОМ = ∠EON как вертикальные, значит

ΔКОМ ~ Δ EON по двум углам.

$\dfrac{KM}{NE}=\dfrac{MO}{NO}$

$KM=\dfrac{MO\cdot NE}{NO}=\dfrac{12\cdot 18}{6}=36$  см

2.

$\dfrac{AB}{A_1B_1}=\dfrac{36}{12}=3$

$\dfrac{BC}{B_1C_1}=\dfrac{33}{11}=3$

У треугольников АВС и А₁В₁С₁:

АВ : А₁В₁ = ВС : В₁С₁

и ∠В = ∠В₁, значит

ΔАВС ~ ΔА₁В₁С₁ по двум пропорциональным сторонам и углу между ними.