Предмет: Алгебра,
автор: ManDadovich
30 БАЛЛОВ решите, пожалуйста, уравнения
Приложения:
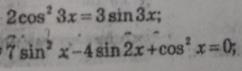
Ответы
Автор ответа:
2
Похожие вопросы
Предмет: Математика,
автор: Tan4ik2
Предмет: Литература,
автор: elenaklimova
Предмет: Русский язык,
автор: Ольга12009
Предмет: Математика,
автор: UlianaMiller18
Предмет: Литература,
автор: lusiLe