Question

Найдите площадь ромба если его острый угол 30 градусов а высота равна 4см​

Answer 1

Ответ:

32 см²

Объяснение:

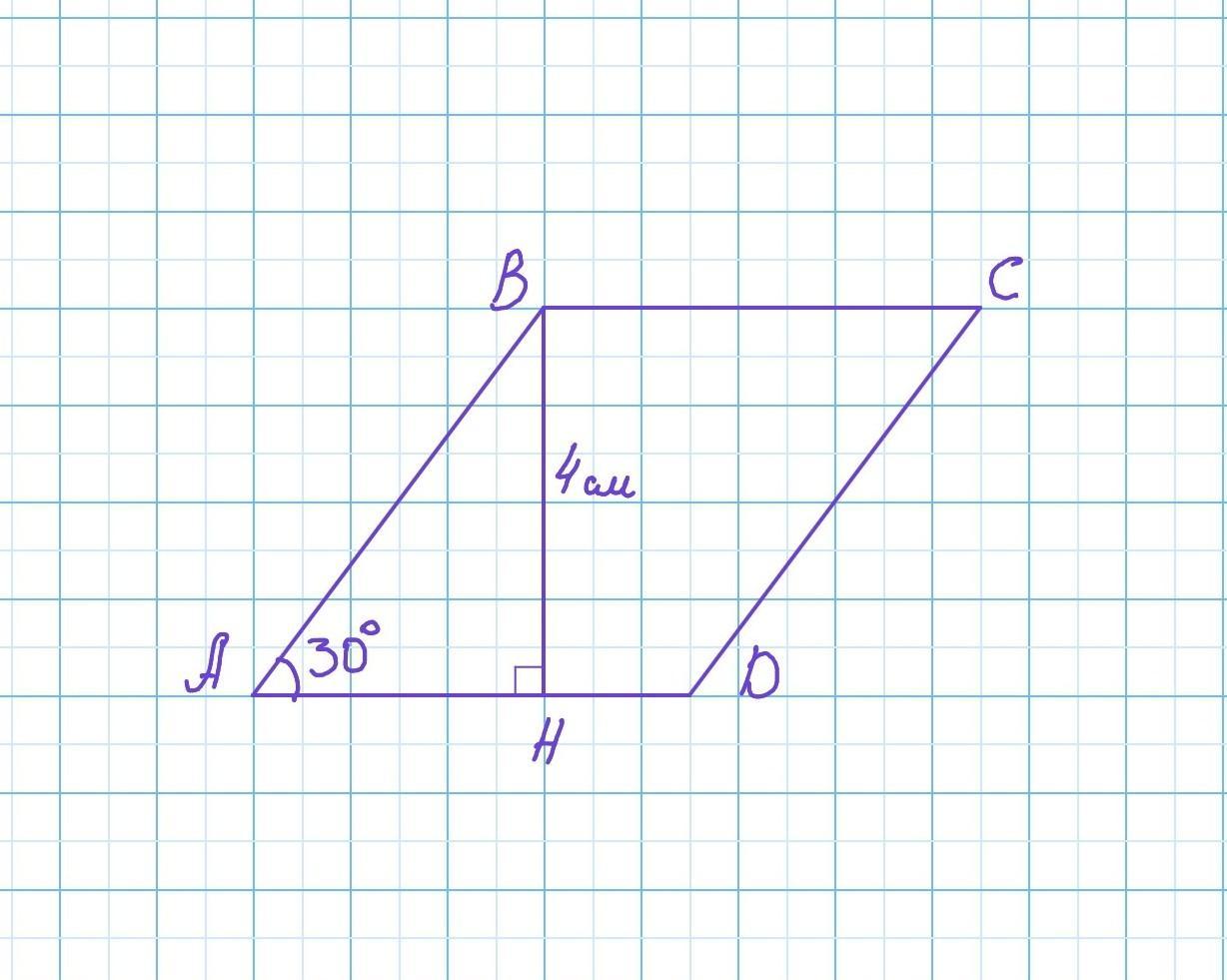
Дано: ABCD - ромб. ∠А=30°. ВН - высота. ВН⟂AD. BH = 4 см

Найти: S(ABCD) - ?

• Площадь ромба равна произведению стороны на высоту ромба: S=a×h

Рассмотрим прямоугольный треугольник АВН.

∠А=30°. Катет ВН = 4 см.

• В прямоугольном треугольнике катет, лежащий напротив угла в 30° равен половине гипотенузы.

Следовательно гипотенуза АВ=2×ВН=2×4=8см.

Так как все стороны ромба равны, то AD=AB=8см.

Находим площадь ромба:

S = AD×BH = 8×4 = 32 см².