Предмет: Алгебра,
автор: Leraleralera151515
Нужно решить неравенство
Приложения:
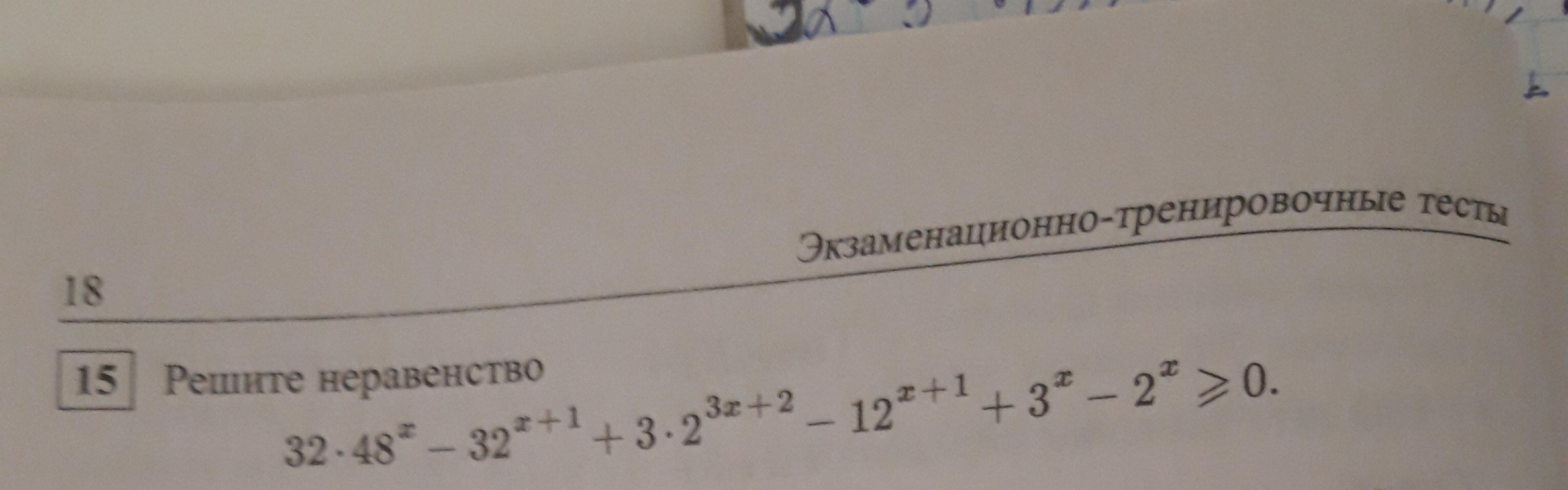
Leraleralera151515:
Поможете? Я упростила, но дальше никак
попробую, а что у вас вышло- на множители не разложили?
Много способов перепробовала
И там не все иксы вошли в общие множители
я порешаю...
там разложение есть
три корня я нашла, осталось методом интервалов найти ответы
у меня вышло так, у вас наверняка ответы есть?
верный
Спасибо Вам!
Ответы
Автор ответа:
1
2^(4x+5)(3^x-2^x)-3*2^(2x+2)(3^x-2^x)+(3^x-2^x)≥0
(3^x-2^x)(2^(4x+5)-3*2^(2x+2)+1)≥0
приравняю к 0 каждый множитель и найду корни
1)3^x-2^x=0; x=0
2)2^(4x+5)-3*2^(2x+2)+1=0
пусть 2^(2x+2)=t
2t^2-3t+1=0
D=9-8=1
t1=(3+1)/4=1; 2^(2x+2)=2^0;2x+2=0;x=-1
t2=(3-1)/4=1/2; 2^(2x+2)=2^(-1); 2x+2=-1;x=-1.5
определю знаки обоих множителях в интервалах
1)---[-1.5]---[-1]----[0]++++
2)++[-1.5]--[-1]++[0]++
тогда ответ x=[-1.5;-1]U[0;+∞)
Похожие вопросы
Предмет: Математика,
автор: dariyash8
Предмет: Математика,
автор: ЯсяД
Предмет: Математика,
автор: shehggssh
Предмет: Математика,
автор: zsarsenbaeva
Предмет: История,
автор: vovasolodovnikov