Предмет: Алгебра,
автор: PRO100ARTEMPRO
Решите графически систему уравнений
y=4x-x^2
2x+y=5
Ответы
Автор ответа:
13
Решить систему уравнений графически.
Первое уравнение в системе:
- квадратичная функция, график - парабола.
- ветви параболы направлены вниз.
Координаты вершины параболы:
Нули функции:
Дополнительные точки для построения:
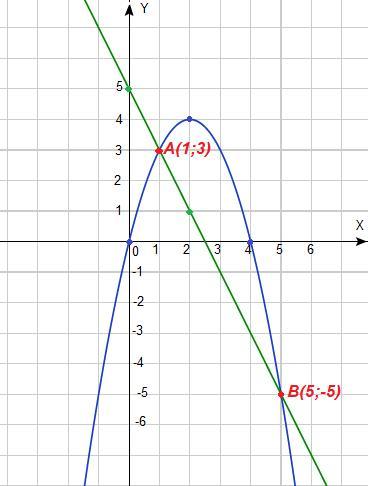
В приложении график синего цвета.
Второе уравнение в системе:
- линейная функция. График - прямая линия.
Для построения достаточно двух точек:
В приложении график зелёного цвета.
Решением системы уравнений являются координаты двух точек пересечения графиков функций:
Ответ: (1; 3), (5; -5).
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Анадана
Предмет: Математика,
автор: Daria2406
Предмет: Алгебра,
автор: tanyusha20
Предмет: Литература,
автор: Аноним
Предмет: Литература,
автор: ivanfilippov11