Question

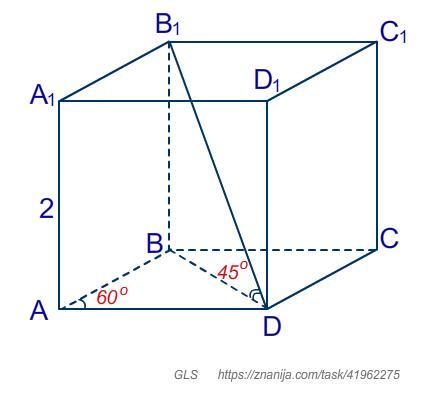
Основанием прямой призмы является ромб, острый угол которого 60 °. Боковое ребро равно 2. Меньшая диагональ призмы составляет с плоскостью основания угол 45 °. Найти объём призмы.

Answer 1

Ответ:

Объем призмы $\displaystyle 4\sqrt {3}$ куб. ед.

Объяснение:

Найти объем призмы, основанием которой является ромб с заданным углом, известными боковым ребром и углом между основанием и меньшей диагональю призмы.

Дано: ABCDA₁B₁C₁D₁ прямая призма; ABCD - ромб (основание призмы); AA₁ = 2; ∠BAD = 60°; 45° - угол между основанием и меньшей диагональю призмы.

Найти: Vпр.

Решение.

Объем призмы равен произведению площади основания на высоту призмы:

S = Sосн · H.

1) Определим высоту призмы.

Так как призма прямая, то боковое ребро ее перпендикулярно основанию и равно высоте призмы.

AA₁ = H = 2.

2) Найдем диагональ BD основания (ромба).

Меньшей наклонной соответствует меньшая проекция.

Меньшей диагональю призмы является та диагональ, проекцией которой является меньшая диагональ ромба - основания призмы.

Диагональ B₁D = 2.

ΔB₁BD прямоугольный с острым углом 45⁰. Тогда ΔB₁BD равнобедренный.

B₁B = BD = 2.

3) Найдем стороны ромба - основания призмы.

Диагональ ромба делит его на два равных равнобедренных треугольника.

Так как острый угол ромба равен 60⁰, то диагональ ромба делит его на два равносторонних треугольника.

ΔABD равносторонний. AB = BD = 2.

Стороны ромба равны по 2 ед.

4) Найдем площадь основания призмы.

Площадь ромба равна произведению квадрата его стороны на синус его угла.

S = a²·sinα.

Площадь основания:

$\displaystyle S = 2^{2} \cdot \sin 60^{o} = 4 \cdot \frac {\sqrt{3}}{2}=2\sqrt{3}$ (кв. ед).

4) Найдем объем призмы.

$\displaystyle V = 2\sqrt{3} \cdot 2 = 4\sqrt {3}$ (куб. ед).

Объем призмы  $\displaystyle 4\sqrt {3}$ куб. единиц.