Предмет: Алгебра,
автор: sobakazabiyaka
Вычислите интеграл

Ответы
Автор ответа:
1
Ответ:
раздели на простейшие дроби с помощью неопределенных коэффициентов
Автор ответа:
0
фотографии в закрепе
заранее извиняюсь за почерк)
Приложения:


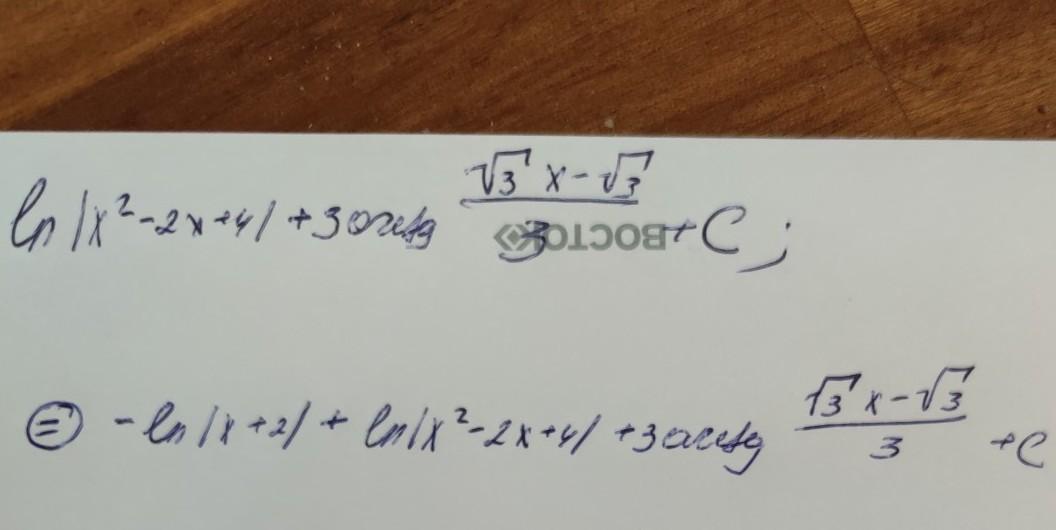
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: alesya300102
Предмет: Математика,
автор: 89297742652
Предмет: Математика,
автор: KoteykaLiza00
Предмет: Литература,
автор: Аноним