Предмет: Математика,
автор: baxa9678
НАЙТИ ПОЛНЫЕ ДИФФЕРЕНЦИАЛЫ УКАЗАННЫХ ФУНКЦИИ
Приложения:
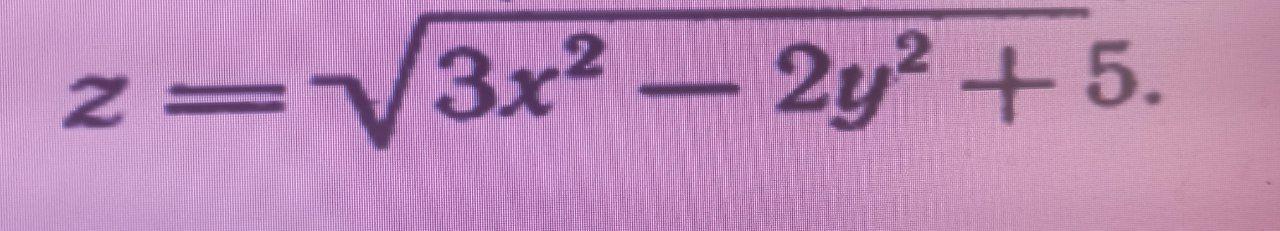
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: История,
автор: NatashaBog
Предмет: Русский язык,
автор: Единорожка1709
Предмет: Математика,
автор: AlikhanKakimov
Предмет: Алгебра,
автор: pha1
Предмет: Математика,
автор: Kddksdcksdkcwd