Предмет: Геометрия,
автор: asswecan
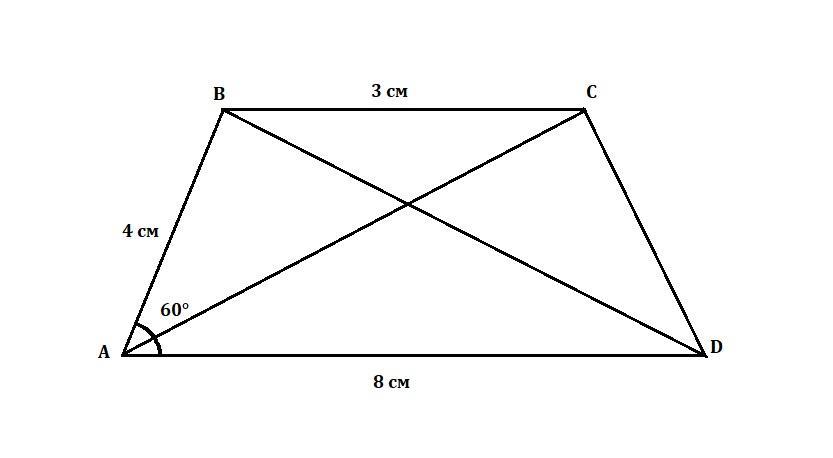
Угол при вершине A трапеции ABCD с основаниями AD и BC равен 60°. Если AD = 8 см, BC = 3 см, AB = 4 см, то найди длины диагонали трапеции.
Приложения:

Ответы
Автор ответа:
1
Ответ:
BD = 4√3 см
АС = √37 см
Объяснение:
1) По теореме косинусов найдём сторону BD в треугольнике АBD:
BD²=АВ²+АD²-2*АВ*АD*соs∠A = 4²+8²-2*4*8*соs 60°=
=16+64-64* = 48
Диагональ BD = √48=4√3 cм
2) Так как сумма углов трапеции, прилежащих к боковой стороне равна 180°, то ∠В = 180°-∠А = 180°-60°=120°.
По теореме косинусов найдём сторону АС в треугольнике АBС:
АС²=АВ²+ВС²-2*АВ*ВС*соs∠В=4²+3²-2*4*3*соs120°=16+9+24 * =37
АС=√37см
Приложения:
Похожие вопросы
Предмет: Обществознание,
автор: gggggj
Предмет: Геометрия,
автор: karicha2000
Предмет: Русский язык,
автор: alekseymartyno4
Предмет: Алгебра,
автор: tolikmirov55
Предмет: Геометрия,
автор: Ideal000584