Предмет: Алгебра,
автор: Pablosss
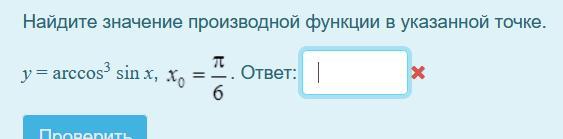
Найдите значение производной функции в указанной точке.
y = arccos³sinx, x0=π/6
Приложения:
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Химия,
автор: ambosh
Предмет: Математика,
автор: xXMalefisentaXx
Предмет: Химия,
автор: hemidovatajan
Предмет: История,
автор: sofeck
Предмет: Геометрия,
автор: NewLordOfTime