Предмет: Алгебра,
автор: cychvj
помогите решить интегралы
Приложения:
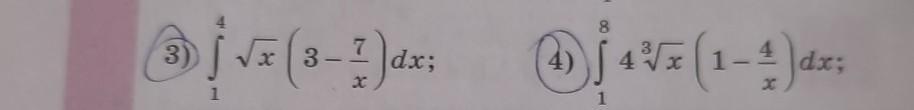
Аноним:
а можно только ответы сказать?
нет
решение нужно
ок
раскрой скобки и смотри в таблицу интегралов - вот и всё решение .........
я не понимаю((
эх
в первом интерграле х=0
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Химия,
автор: влад1999912
Предмет: Биология,
автор: ArinaBlare
Предмет: Русский язык,
автор: марсий
Предмет: Математика,
автор: rohkova33
Предмет: Литература,
автор: Lera561111