Предмет: Алгебра,
автор: polina2003000000
ГЛАВНЫЙ МОЗГ,СПАСИ,10 КЛАСС,АЛГЕБРА
Приложения:
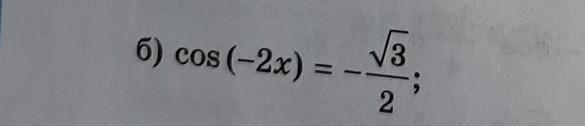
Ответы
Автор ответа:
3
Для того чтобы решить уравнение вида , где
, нужно воспользоваться формулой:
Пусть . Тогда имеем:
Здесь
Имеем:
Обратная замена:
Так как , то
Ответ:
polina2003000000:
a откуда там t?
ой,всё,тупанула,простите:)
Похожие вопросы
Предмет: Алгебра,
автор: Alinagilmor
Предмет: Алгебра,
автор: bobyleva20
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: ОстровскаяМария1
Предмет: Физика,
автор: marichamaricha